34

Learning Objectives

  • Set up and solve optimization problems in several applied fields.

One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.

Solving Optimization Problems over a Closed, Bounded Interval

The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in (Figure) , we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.

Maximizing the Area of a Garden

A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides ( (Figure) ). Given 100 ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?

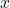A drawing of a garden has x and y written on the vertical and horizontal sides, respectively. There is a rock wall running along the entire bottom horizontal length of the drawing.
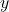Figure 1. We want to determine the measurements x and y that will create a garden with a maximum area using 100 ft of fencing.

Solution

Let x denote the length of the side of the garden perpendicular to the rock wall and y denote the length of the side parallel to the rock wall. Then the area of the garden is

A=x\cdoty.

We want to find the maximum possible area subject to the constraint that the total fencing is 100\text{ft}. From (Figure) , the total amount of fencing used will be 2x+y. Therefore, the constraint equation is

2x+y=100.

Solving this equation for y, we have y=100-2x. Thus, we can write the area as

A(x)=x\cdot(100-2x)=100x-2{x}^{2}.

Before trying to maximize the area function A(x)=100x-2{x}^{2}, we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need x \symbol{"3E} 0 and y \symbol{"3E} 0. Since y=100-2x, if y \symbol{"3E} 0, then x<50. Therefore, we are trying to determine the maximum value of A(x) for x over the open interval (0,50). We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function A(x)=100x-2{x}^{2} over the closed interval \left[0,50\right]. If the maximum value occurs at an interior point, then we have found the value x in the open interval (0,50) that maximizes the area of the garden. Therefore, we consider the following problem:

Maximize A(x)=100x-2{x}^{2} over the interval \left[0,50\right].

As mentioned earlier, since A is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical numbers. At the endpoints, A(x)=0. Since the area is positive for all x in the open interval (0,50), the maximum must occur at a critical number. Differentiating the function A(x), we obtain

{A}^{\prime }(x)=100-4x.

Therefore, the only critical number is x=25 ( (Figure) ). We conclude that the maximum area must occur when x=25. Then we have y=100-2x=100-2(25)=50. To maximize the area of the garden, let x=25 ft and y=50\text{ft}. The area of this garden is 1250{\text{ft}}^{2}.

The function A(x) = 100x – 2x is graphed. At its maximum there is an intersection of two dashed lines and text that reads “Maximum area is 1250 square feet when x = 25 feet.”
Figure 2. To maximize the area of the garden, we need to find the maximum value of the function A(x)=100x-2{x}^{2}.

Determine the maximum area if we want to make the same rectangular garden as in (Figure) , but we have 200 ft of fencing.

Hint

We need to maximize the function A(x)=200x-2{x}^{2} over the interval \left[0,100\right].

Solution

The maximum area is 5000{\text{ft}}^{2}.

 

Now let’s look at a general strategy for solving optimization problems similar to (Figure) .

Problem-Solving Strategy: Solving Optimization Problems

  1. Introduce all variables. If applicable, draw a figure and label all variables.
  2. Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
  3. Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable.
  4. Write any equations relating the independent variables in the formula from step 3. Use these equations to write the quantity to be maximized or minimized as a function of one variable.
  5. Identify the domain of consideration for the function in step 4 based on the physical problem to be solved.
  6. Locate the maximum or minimum value of the function from step 4. This step typically involves looking for critical numbers. Justify the answer using the closed interval method or another method if the interval is not closed.
  7. Give the final answer as a sentence with units.

Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.

Maximizing the Volume of a Box

An open-top box is to be made from a 24 in. by 36 in. piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?

Solution

Step 1: Let x be the side length of the square to be removed from each corner ( (Figure) ). Then, the remaining four flaps can be folded up to form an open-top box. Let V be the volume of the resulting box.

There are two figures for this figure. The first one is a rectangle with sides 24 in and 36 in, with each corner having a square of side length x taken out of it. In the second picture, there is a box with side lengths x in, 24 – 2x in, and 36 – 2x in.
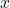Figure 3. A square with side length x inches is removed from each corner of the piece of cardboard. The remaining flaps are folded to form an open-top box.

Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize V.

Step 3: As mentioned in step 2, are trying to maximize the volume of a box. The volume of a box is V=L\cdotW\cdotH, where L,W,\text{ and }H are the length, width, and height, respectively.

Step 4: From (Figure) , we see that the height of the box is x inches, the length is 36-2x inches, and the width is 24-2x inches. Therefore, the volume of the box is

V(x)=(36-2x)(24-2x)x=4{x}^{3}-120{x}^{2}+864x.

Step 5: To determine the domain of consideration, let’s examine (Figure) . Certainly, we need x \symbol{"3E} 0. Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, 24 in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for x over the open interval (0,12). Since V is a continuous function over the closed interval \left[0,12\right], we know V will have an absolute maximum over the closed interval. Therefore, we consider V over the closed interval \left[0,12\right] and check whether the absolute maximum occurs at an interior point.

Step 6: Since V(x) is a continuous function over the closed, bounded interval \left[0,12\right], V must have an absolute maximum (and an absolute minimum). Since V(x)=0 at the endpoints and V(x) \symbol{"3E} 0 for 0<x<12, the maximum must occur at a critical number. The derivative is

{V}^{\prime }(x)=12{x}^{2}-240x+864.

To find the critical numbers, we need to solve the equation

12{x}^{2}-240x+864=0.

Dividing both sides of this equation by 12, the problem simplifies to solving the equation

{x}^{2}-20x+72=0.

Using the quadratic formula, we find that the critical numbers are

x=\frac{20\pm \sqrt{{(-20)}^{2}-4(1)(72)}}{2}=\frac{20\pm \sqrt{112}}{2}=\frac{20\pm 4\sqrt{7}}{2}=10\pm 2\sqrt{7}.

Since 10+2\sqrt{7} is not in the domain of consideration, the only critical number we need to consider is 10-2\sqrt{7}. Therefore, the volume is maximized if we let x=10-2\sqrt{7}\text{in}. The maximum volume is V(10-2\sqrt{7})=640+448\sqrt{7}\approx 1825\text{in}{.}^{3} as shown in the following graph.

The function V(x) = 4x3 – 120x2 + 864x is graphed. At its maximum there is an intersection of two dashed lines and text that reads “Maximum volume is approximately 1825 cubic inches when x ≈ 4.7 inches.”
Figure 4. Maximizing the volume of the box leads to finding the maximum value of a cubic polynomial.

Watch a video about optimizing the volume of a box.

Suppose the dimensions of the cardboard in (Figure) are 20 in. by 30 in. Let x be the side length of each square and write the volume of the open-top box as a function of x. Determine the domain of consideration for x.

Hint

The volume of the box is L\cdotW\cdotH.

Solution

V(x)=x(20-2x)(30-2x). The domain is \left[0,10\right].

Minimizing Travel Time

An island is 2\text{mi} due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 6\text{mi} west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of 8\text{mph} and swims at a rate of 3\text{mph}. How far should the visitor run before swimming to minimize the time it takes to reach the island?

Solution

Step 1: Let x be the distance running and let y be the distance swimming ( (Figure) ). Let T be the time it takes to get from the cabin to the island.

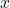The cabin is x miles from the shore. From that point on the shore, the island is y miles away. If you were to continue the line from the cabin to the shore (the x miles one) and if you were to draw a line from the island parallel to the shore, then the lines would extend 2 miles from the island and 6 miles from the cabin before intersecting.
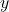Figure 5. How can we choose x and y to minimize the travel time from the cabin to the island?

Step 2: The problem is to minimize T.

Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time (D=R×T), the time spent running is

{T}_{\text{running}}=\frac{{D}_{\text{running}}}{{R}_{\text{running}}}=\frac{x}{8},

and the time spent swimming is

{T}_{\text{swimming}}=\frac{{D}_{\text{swimming}}}{{R}_{\text{swimming}}}=\frac{y}{3}.

Therefore, the total time spent traveling is

T=\frac{x}{8}+\frac{y}{3}.

Step 4: From (Figure) , the line segment of y miles forms the hypotenuse of a right triangle with legs of length 2\text{mi} and 6-x\text{mi}. Therefore, by the Pythagorean theorem, {2}^{2}+{(6-x)}^{2}={y}^{2}, and we obtain y=\sqrt{{(6-x)}^{2}+4}. Thus, the total time spent traveling is given by the function

T(x)=\frac{x}{8}+\frac{\sqrt{{(6-x)}^{2}+4}}{3}.

Step 5: From (Figure) , we see that 0\le x\le 6. Therefore, \left[0,6\right] is the domain of consideration.

Step 6: Since T(x) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical numbers of T over the interval \left[0,6\right]. The derivative is

{T}^{\prime }(x)=\frac{1}{8}-\frac{1}{2}\frac{{\left[{(6-x)}^{2}+4\right]}^{-1\text{/}2}}{3}\cdot2(6-x)=\frac{1}{8}-\frac{(6-x)}{3\sqrt{{(6-x)}^{2}+4}}.

If {T}^{\prime }(x)=0, then

\frac{1}{8}=\frac{6-x}{3\sqrt{{(6-x)}^{2}+4}}.

Therefore,

3\sqrt{{(6-x)}^{2}+4}=8(6-x).

Squaring both sides of this equation, we see that if x satisfies this equation, then x must satisfy

9\left[{(6-x)}^{2}+4\right]=64{(6-x)}^{2},

which implies

55{(6-x)}^{2}=36.

We conclude that if x is a critical number, then x satisfies

{(x-6)}^{2}=\frac{36}{55}.

Therefore, the possibilities for critical numbers are

x=6\pm \frac{6}{\sqrt{55}}.

Since x=6+6\text{/}\sqrt{55} is not in the domain, it is not a possibility for a critical number. On the other hand, x=6-6\text{/}\sqrt{55} is in the domain. Since we squared both sides of (Figure) to arrive at the possible critical numbers, it remains to verify that x=6-6\text{/}\sqrt{55} satisfies (Figure) . Since x=6-6\text{/}\sqrt{55} does satisfy that equation, we conclude that x=6-6\text{/}\sqrt{55} is a critical number, and it is the only one. To justify that the time is minimized for this value of x, we just need to check the values of T(x) at the endpoints x=0 and x=6, and compare them with the value of T(x) at the critical number x=6-6\text{/}\sqrt{55}. We find that T(0)\approx 2.108\text{h} and T(6)\approx 1.417\text{h,} whereas T(6-6\text{/}\sqrt{55})\approx 1.368\text{h}. Therefore, we conclude that T has a local minimum at x\approx 5.19 mi.

Suppose the island is 1 mi from shore, and the distance from the cabin to the point on the shore closest to the island is 15\text{mi}. Suppose a visitor swims at the rate of 2.5\text{mph} and runs at a rate of 6\text{mph}. Let x denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.

Hint

The time T={T}_{\text{running}}+{T}_{\text{swimming}}.

Solution

T(x)=\frac{x}{6}+\frac{\sqrt{{(15-x)}^{2}+1}}{2.5}

 

In business, companies are interested in maximizing revenue . In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.

Maximizing Revenue

Owners of a car rental company have determined that if they charge customers p dollars per day to rent a car, where 50\le p\le 200, the number of cars n they rent per day can be modeled by the linear function n(p)=1000-5p. If they charge $50 per day or less, they will rent all their cars. If they charge $200 per day or more, they will not rent any cars. Assuming the owners plan to charge customers between $50 per day and $200 per day to rent a car, how much should they charge to maximize their revenue?

Solution

Step 1: Let p be the price charged per car per day and let n be the number of cars rented per day. Let R be the revenue per day.

Step 2: The problem is to maximize R.

Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, R=n×p.

Step 4: Since the number of cars rented per day is modelled by the linear function n(p)=1000-5p, the revenue R can be represented by the function

R(p)=n×p=(1000-5p)p=-5{p}^{2}+1000p.

Step 5: Since the owners plan to charge between \$50 per car per day and \$200 per car per day, the problem is to find the maximum revenue R(p) for p in the closed interval \left[50,200\right].

Step 6: Since R is a continuous function over the closed, bounded interval \left[50,200\right], it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical numbers. The derivative is {R}^{\prime }(p)=-10p+1000. Therefore, the critical number is p=100 When p=100, R(100)=\$50,000. When p=50, R(p)=\$37,500. When p=200, R(p)=\$0. Therefore, the absolute maximum occurs at p=\$100. The car rental company should charge \$100 per day per car to maximize revenue as shown in the following figure.

The function R(p) is graphed. At its maximum there is an intersection of two dashed lines and text that reads “Maximum revenue is 💲50,000 per day when the price charged per car is 💲100 per day.”
Figure 6. To maximize revenue, a car rental company has to balance the price of a rental against the number of cars people will rent at that price.

A car rental company charges its customers p dollars per day, where 60\le p\le 150. It has found that the number of cars rented per day can be modelled by the linear function n(p)=750-5p. How much should the company charge each customer to maximize revenue?

Hint

R(p)=n×p, where n is the number of cars rented and p is the price charged per car.

Solution

The company should charge $75 per car per day.

Maximizing the Area of an Inscribed Rectangle

A rectangle is to be inscribed in the ellipse

\frac{{x}^{2}}{4}+{y}^{2}=1.

What should the dimensions of the rectangle be to maximize its area? What is the maximum area?

Solution

Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let L be the length of the rectangle and W be its width. Let A be the area of the rectangle.

The ellipse x2/4 + y2 = 1 is drawn with its x intercepts being ±2 and its y intercepts being ±1. There is a rectangle inscribed in the ellipse with length L (in the x-direction) and width W.
Figure 7. We want to maximize the area of a rectangle inscribed in an ellipse.

Step 2: The problem is to maximize A.

Step 3: The area of the rectangle is A=LW.

Step 4: Let (x,y) be the corner of the rectangle that lies in the first quadrant, as shown in (Figure) . We can write length L=2x and width W=2y. Since \frac{{x}^{2}}{4+{y}^{2}=1} and y \symbol{"3E} 0, we have y=\sqrt{\frac{1-{x}^{2}}{4}}. Therefore, the area is

A=LW=(2x)(2y)=4x\sqrt{\frac{1-{x}^{2}}{4}}=2x\sqrt{4-{x}^{2}}.

Step 5: From (Figure) , we see that to inscribe a rectangle in the ellipse, the x-coordinate of the corner in the first quadrant must satisfy 0<x<2. Therefore, the problem reduces to looking for the maximum value of A(x) over the open interval (0,2). Since A(x) will have an absolute maximum (and absolute minimum) over the closed interval \left[0,2\right], we consider A(x)=2x\sqrt{4-{x}^{2}} over the interval \left[0,2\right]. If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.

Step 6: As mentioned earlier, A(x) is a continuous function over the closed, bounded interval \left[0,2\right]. Therefore, it has an absolute maximum (and absolute minimum). At the endpoints x=0 and x=2, A(x)=0. For 0<x<2, A(x) \symbol{"3E} 0. Therefore, the maximum must occur at a critical number. Taking the derivative of A(x), we obtain

\begin{array}{cc}\hfill A\prime (x)& =2\sqrt{4-{x}^{2}}+2x\cdot\frac{1}{2\sqrt{4-{x}^{2}}}(-2x)\hfill \\ & =2\sqrt{4-{x}^{2}}-\frac{2{x}^{2}}{\sqrt{4-{x}^{2}}}\hfill \\ & =\frac{8-4{x}^{2}}{\sqrt{4-{x}^{2}}}.\hfill \end{array}

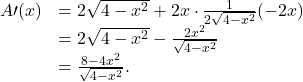
To find critical numbers, we need to find where A\prime (x)=0. We can see that if x is a solution of

\frac{8-4{x}^{2}}{\sqrt{4-{x}^{2}}}=0,

then x must satisfy

8-4{x}^{2}=0.

Therefore, {x}^{2}=2. Thus, x=\pm \sqrt{2} are the possible solutions of (Figure) . Since we are considering x over the interval \left[0,2\right], x=\sqrt{2} is a possibility for a critical number, but x=-\sqrt{2} is not. Therefore, we check whether \sqrt{2} is a solution of (Figure) . Since x=\sqrt{2} is a solution of (Figure) , we conclude that \sqrt{2} is the only critical number of A(x) in the interval \left[0,2\right]. Therefore, A(x) must have an absolute maximum at the critical number x=\sqrt{2}. To determine the dimensions of the rectangle, we need to find the length L and the width W. If x=\sqrt{2} then

y=\sqrt{1-\frac{{(\sqrt{2})}^{2}}{4}}=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}.

Therefore, the dimensions of the rectangle are L=2x=2\sqrt{2} and W=2y=\frac{2}{\sqrt{2}}=\sqrt{2}. The area of this rectangle is A=LW=(2\sqrt{2})(\sqrt{2})=4.

Modify the area function A if the rectangle is to be inscribed in the unit circle {x}^{2}+{y}^{2}=1. What is the domain of consideration?

Hint

If (x,y) is the vertex of the square that lies in the first quadrant, then the area of the square is A=(2x)(2y)=4xy.

Solution

A(x)=4x\sqrt{1-{x}^{2}}. The domain of consideration is \left[0,1\right].

Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded

In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.

Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function f(x)={x}^{2}+4 over (-\infty ,\infty ) has an absolute minimum of 4 at x=0. Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is (0,\infty ), the function has an absolute minimum. Below are the options to justify an absolute maximum or minimum of a continuous function on an open interval.

Problem-Solving Strategy: Justify a Maximum or Minimum on an Open Interval

  1. Instead of testing the endpoints, take the limit as the variable approaches the endpoint. If both those answers are less than a critical number, then the largest function value at the critical numbers is the absolute maximum. Similar for minimum. If at least one of the limits is larger than all function values at the critical numbers (or is infinity), then there is no maximum. Similar for minimum.
  2. If the function is increasing over the entire interval to the left of the critical number and decreasing for the entire interval after the critical number, then there is the absolute maximum at the critical number. Similar for minimum.
  3. If there is only one critical number on the interval and there is a local maximum at that value, then there is an absolute maximum at that value. Similar for minimum.

In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.

Minimizing Surface Area

A rectangular box with a square base, an open top, and a volume of 216 in. 3 is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?

Solution

Step 1: Draw a rectangular box and introduce the variable x to represent the length of each side of the square base; let y represent the height of the box. Let S denote the surface area of the open-top box.

A box with square base is shown. The base has side length x, and the height is y.
Figure 8. We want to minimize the surface area of a square-based box with a given volume.

Step 2: We need to minimize the surface area. Therefore, we need to minimize S.

Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is x\cdoty. The area of the base is {x}^{2}. Therefore, the surface area of the box is

S=4xy+{x}^{2}.

Step 4: Since the volume of this box is {x}^{2}y and the volume is given as 216\text{in}{.}^{3}, the constraint equation is

{x}^{2}y=216.

Solving the constraint equation for y, we have y=\frac{216}{{x}^{2}}. Therefore, we can write the surface area as a function of x only:

S(x)=4x(\frac{216}{{x}^{2}})+{x}^{2}.

Therefore, S(x)=\frac{864}{x}+{x}^{2}.

Step 5: Since we are requiring that {x}^{2}y=216, we cannot have x=0. Therefore, we need x \symbol{"3E} 0. On the other hand, x is allowed to have any positive value. Note that as x becomes large, the height of the box y becomes correspondingly small so that {x}^{2}y=216. Similarly, as x becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval (0,\infty ). Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval (0,\infty ).

Step 6: Note that as x\to {0}^{+}, S(x)\to \infty . Also, as x\to \infty , S(x)\to \infty . Since S is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some x\in (0,\infty ). This minimum must occur at a critical number of S. The derivative is

{S}^{\prime }(x)=-\frac{864}{{x}^{2}}+2x.

Therefore, {S}^{\prime }(x)=0 when 2x=\frac{864}{{x}^{2}}. Solving this equation for x, we obtain {x}^{3}=432, so x=\sqrt[3]{432}=6\sqrt[3]{2}. Since this is the only critical number of S, the absolute minimum must occur at x=6\sqrt[3]{2} (see (Figure) ). When x=6\sqrt[3]{2}, y=\frac{216}{{(6\sqrt[3]{2})}^{2}}=3\sqrt[3]{2}\text{in}. Therefore, the dimensions of the box should be x=6\sqrt[3]{2}\text{in}. and y=3\sqrt[3]{2}\text{in}. With these dimensions, the surface area is

S(6\sqrt[3]{2})=\frac{864}{6\sqrt[3]{2}}+{(6\sqrt[3]{2})}^{2}=108\sqrt[3]{4}\text{in}{.}^{2}
The function S(x) = 864/x + x2 is graphed. At its minimum there is a dashed line and text that reads “Minimum surface area is 108 times the cube root of 4 square inches when x = 6 times the cube root of 2 inches.”
Figure 9. We can use a graph to determine the dimensions of a box of given the volume and the minimum surface area.

Alternative to Step 6: As we saw before, x=6\sqrt[3]{2} is the only critical number of the function on our interval. Hence we can use the first or second derivative test to determine whether we have an absolute minimum. Taking the second derivative we get S^{\prime\prime }(x) = \frac{1728}{x^3}+2 which is positive at our critical number. Therefore we get a local minimum at our critical number. Since it’s the only critical number on our interval, it’s an absolute minimum. Therefore the minimum surface area is 108\sqrt[3]{4}\text{in}{.}^{2}

Consider the same open-top box, which is to have volume 216\text{in}{.}^{3}. Suppose the cost of the material for the base is 20¢\text{/}\text{in}{.}^{2} and the cost of the material for the sides is 30¢\text{/}\text{in}{.}^{2} and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let x be the side length of the base and y be the height of the box.)

Hint

If the cost of one of the sides is 30¢\text{/}\text{in}{.}^{2}, the cost of that side is 0.30xy.

Solution

c(x)=\frac{259.2}{x}+0.2{x}^{2} dollars

Key Concepts

  • To solve an optimization problem, begin by drawing a picture and introducing variables.
  • Find an equation relating the variables.
  • Find a function of one variable to describe the quantity that is to be minimized or maximized.
  • Look for critical numbers to locate local extrema.

For the following exercises, answer by proof, counterexample, or explanation.

1. When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical numbers?

Solution

The critical numbers can be the minima, maxima, or neither.

2. Why do you need to check the endpoints for optimization problems?

3. True or False . For every continuous nonlinear function, you can find the value x that maximizes the function.

Solution

False; y={x}^{2} has a minimum only

4. True or False . For every continuous non-constant function on a closed, finite domain, there exists at least one x that minimizes or maximizes the function.

For the following exercises, set up and evaluate each optimization problem.

5. To carry a suitcase on an airplane, the length +\text{width}+ height of the box must be less than or equal to 62\text{in}. Assuming the height is fixed, show that the maximum volume is V=h{(31-(\frac{1}{2})h)}^{2}. What height allows you to have the largest volume?

Solution

h=\frac{62}{3} in.

6. You are constructing a cardboard box with the dimensions \text{2 m by 4 m}. You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?

A rectangle is drawn with height 2 and width 4. Each corner has a square with side length x marked on it.

7. Find the positive integer that minimizes the sum of the number and its reciprocal.

Solution

1

8. Find two positive integers such that their sum is 10, and minimize and maximize the sum of their squares.

For the following exercises, consider the construction of a pen to enclose an area.

9. You have 400\text{ft} of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?

Solution

100\text{ft by}100\text{ft}

10. You have 800\text{ft} of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?

11. You need to construct a fence around an area of 1600\text{ft}. What are the dimensions of the rectangular pen to minimize the amount of material needed?

Solution

40\text{ft by}40\text{ft}

12. Two poles are connected by a wire that is also connected to the ground. The first pole is 20\text{ft} tall and the second pole is 10\text{ft} tall. There is a distance of 30\text{ft} between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?

Two poles are shown, one that is 10 tall and the other is 20 tall. A right triangle is made with the shorter pole with other side length x. The distance between the two poles is 30.

13. [T] You are moving into a new apartment and notice there is a corner where the hallway narrows from \text{8 ft to 6 ft}. What is the length of the longest item that can be carried horizontally around the corner?

An upside L-shaped figure is drawn with the _ part being 6 wide and the | part being 8 wide. There is a line drawn from the _ part to the | part that touches the near corner of the shape to form a hypotenuse for a right triangle the other sides being the the rest of the _ and | parts. This line is marked L.

Solution

19.73\text{ft}.

14. A patient’s pulse measures \text{70 bpm, 80 bpm, then 120 bpm}. To determine an accurate measurement of pulse, the doctor wants to know what value minimizes the expression {(x-70)}^{2}+{(x-80)}^{2}+{(x-120)}^{2}? What value minimizes it?

15. In the previous problem, assume the patient was nervous during the third measurement, so we only weight that value half as much as the others. What is the value that minimizes {(x-70)}^{2}+{(x-80)}^{2}+\frac{1}{2}{(x-120)}^{2}?

Solution

84\text{bpm}

16. You can run at a speed of 6 mph and swim at a speed of 3 mph and are located on the shore, 4 miles east of an island that is 1 mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?

A rectangle is drawn that has height 1 and length 4. In the lower right corner, it is marked “You” and in the upper left corner it is marked “Island.”

For the following problems, consider a lifeguard at a circular pool with diameter 40\text{m}. He must reach someone who is drowning on the exact opposite side of the pool, at position C. The lifeguard swims with a speed v and runs around the pool at speed w=3v.

A circle is drawn with points A and C on a diameter. There is a point B drawn on the circle such that angle BAC form an acute angle θ.

17. Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, \theta .

Solution

T(\theta )=\frac{40\theta }{3v}+\frac{40 \cos \theta }{v}

18. Find at what angle \theta the lifeguard should swim to reach the drowning person in the least amount of time.

19. A truck uses gas as g(v)=av+\frac{b}{v}, where v represents the speed of the truck and g represents the gallons of fuel per mile. At what speed is fuel consumption minimized?

Solution

v=\sqrt{\frac{b}{a}}

For the following exercises, consider a limousine that gets m(v)=\frac{(120-2v)}{5}\text{mi/gal} at speed v, the chauffeur costs {$15/h} and gas is $3.5\text{/}\text{gal}.

20. Find the cost per mile at speed v.

21. Find the cheapest driving speed.

Solution

approximately 34.02\text{mph}

For the following exercises, consider a pizzeria that sell pizzas for a revenue of R(x)=ax and costs C(x)=b+cx+d{x}^{2}, where x represents the number of pizzas.

22. Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?

23. Assume that R(x)=10x and C(x)=2x+{x}^{2}. How many pizzas sold maximizes the profit?

Solution

4

24. Assume that R(x)=15x, and C(x)=60+3x+\frac{1}{2}{x}^{2}. How many pizzas sold maximizes the profit?

For the following exercises, consider a wire 4\text{ft} long cut into two pieces. One piece forms a circle with radius r and the other forms a square of side x.

25. Choose x to maximize the sum of their areas.

Solution

0

26. Choose x to minimize the sum of their areas.

For the following exercises, consider two nonnegative numbers x and y such that x+y=10. Maximize and minimize the quantities.

27. xy

Solution

Maximal: x=5,y=5; minimal: x=0,y=10 and y=0,x=10

28. {x}^{2}{y}^{2}

29. y-\frac{1}{x}

Solution

Maximal: x=1,y=9; minimal: none

30. {x}^{2}-y

For the following exercises, draw the given optimization problem and solve.

31. Find the volume of the largest right circular cylinder that fits in a sphere of radius 1.

Solution

\frac{4\pi }{3\sqrt{3}}

32. Find the volume of the largest right cone that fits in a sphere of radius 1.

33. Find the area of the largest rectangle that fits into the triangle with sides x=0,y=0 and \frac{x}{4}+\frac{y}{6}=1.

Solution

6

34. Find the largest volume of a cylinder that fits into a cone that has base radius R and height h.

35. Find the dimensions of the closed cylinder volume V=16\pi that has the least amount of surface area.

Solution

r=2,h=4

36. Find the dimensions of a right cone with surface area S=4\pi that has the largest volume.

For the following exercises, consider the points on the given graphs. Use a calculator to graph the functions.

37. [T] Where is the line y=5-2x closest to the origin?

Solution

(2,1)

38. [T] Where is the line y=5-2x closest to point (1,1)?

39. [T] Where is the parabola y={x}^{2} closest to point (2,0)?

Solution

(0.8351,0.6974)

40. [T] Where is the parabola y={x}^{2} closest to point (0,3)?

For the following exercises, set up, but do not evaluate, each optimization problem.

41. A window is composed of a semicircle placed on top of a rectangle. If you have 20\text{ft} of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use r to represent the radius of the semicircle.

A semicircular window is drawn with radius r.

Solution

A=20r-2{r}^{2}-\frac{1}{2}\pi {r}^{2}

42. You have a garden row of 20 watermelon plants that produce an average of 30 watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?

43. You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs $5\text{/}{\text{ft}}^{2} and the material for the sides costs $2\text{/}{\text{ft}}^{2}. You need a box with volume 4{\text{ft}}^{2}. Find the dimensions of the box that minimize cost. Use x to represent the length of the side of the box.

Solution

C(x)=5{x}^{2}+\frac{32}{x}

44. You are building five identical pens adjacent to each other with a total area of 1000{\text{m}}^{2}, as shown in the following figure. What dimensions should you use to minimize the amount of fencing?

A rectangle is divided into five sections, and each section has length y and width x.

45. You are the manager of an apartment complex with 50 units. When you set rent at $800\text{/}\text{month,} all apartments are rented. As you increase rent by $25\text{/}\text{month,} one fewer apartment is rented. Maintenance costs run $50\text{/}\text{month} for each occupied unit. What is the rent that maximizes the total amount of profit?

Solution

P(x)=(50-x)(800+25x-50)

Glossary

optimization problems
problems that are solved by finding the maximum or minimum value of a function

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Calculus Volume 1 Copyright © 2016 by OSCRiceUniversity is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book