28
Learning Objectives
- Analyze a function and its derivatives to draw its graph.
We have shown how to use the first and second derivatives of a function to describe the shape of a graph. Now we put everything together with other features to graph a function ![]() .
.
Guidelines for Drawing the Graph of a Function
We now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. Before showing how to graph specific functions, let’s look at a general strategy to use when graphing any function.
Problem-Solving Strategy: Drawing the Graph of a Function
Given a function ![]() use the following steps to sketch a graph of
use the following steps to sketch a graph of ![]()
- Determine the domain of the function.
- Locate the
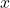 – and
– and 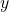 -intercepts.
-intercepts. - Evaluate
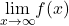 and
and 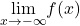 to determine horizontal or oblique asymptote.
to determine horizontal or oblique asymptote. - Determine whether
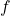 has any vertical asymptotes.
has any vertical asymptotes. - Calculate
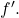 Find all critical numbers and determine the intervals where
Find all critical numbers and determine the intervals where 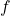 is increasing and where
is increasing and where 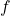 is decreasing. Determine whether
is decreasing. Determine whether 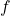 has any local extrema.
has any local extrema. - Calculate
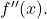 Determine the intervals where
Determine the intervals where 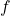 is concave up and where
is concave up and where 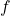 is concave down. Use this information to determine whether
is concave down. Use this information to determine whether 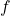 has any inflection points. The second derivative can also be used as an alternate means to determine or verify that
has any inflection points. The second derivative can also be used as an alternate means to determine or verify that 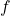 has a local extremum at a critical number.
has a local extremum at a critical number.
Now let’s use this strategy to graph several different functions. We start by graphing a polynomial function.
Sketching a Graph of a Polynomial
Sketch a graph of ![]()
Solution
Step 1. Since ![]() is a polynomial, the domain is the set of all real numbers.
is a polynomial, the domain is the set of all real numbers.
Step 2. When ![]() Therefore, the
Therefore, the ![]() -intercept is
-intercept is ![]() To find the
To find the ![]() -intercepts, we need to solve the equation
-intercepts, we need to solve the equation ![]() gives us the
gives us the ![]() -intercepts
-intercepts ![]() and
and ![]()
Step 3. We need to evaluate the end behavior of ![]() As
As ![]()
![]() and
and ![]() Therefore,
Therefore, ![]() As
As ![]()
![]() and
and ![]() Therefore,
Therefore, ![]()
Step 4. Since ![]() is a polynomial function, it does not have any vertical asymptotes.
is a polynomial function, it does not have any vertical asymptotes.
Step 5. The first derivative of ![]() is
is
Therefore, ![]() has two critical numbers:
has two critical numbers: ![]() Divide the interval
Divide the interval ![]() into the three smaller intervals:
into the three smaller intervals: ![]()
![]() and
and ![]() Then, choose test points
Then, choose test points ![]()
![]() and
and ![]() from these intervals and evaluate the sign of
from these intervals and evaluate the sign of ![]() at each of these test points, as shown in the following table.
at each of these test points, as shown in the following table.
| Interval | Test Point | Sign of Derivative |
Conclusion |
|---|---|---|---|
From the table, we see that ![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() Evaluating
Evaluating ![]() at those two points, we find that the local maximum value is
at those two points, we find that the local maximum value is ![]() and the local minimum value is
and the local minimum value is ![]()
Step 6. The second derivative of ![]() is
is
The second derivative is zero at ![]() Therefore, to determine the concavity of
Therefore, to determine the concavity of ![]() divide the interval
divide the interval ![]() into the smaller intervals
into the smaller intervals ![]() and
and ![]() and choose test points
and choose test points ![]() and
and ![]() to determine the concavity of
to determine the concavity of ![]() on each of these smaller intervals as shown in the following table.
on each of these smaller intervals as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
We note that the information in the preceding table confirms the fact, found in step 5, that ![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() In addition, the information found in step 5—namely,
In addition, the information found in step 5—namely, ![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() and
and ![]() at those points—combined with the fact that
at those points—combined with the fact that ![]() changes sign only at
changes sign only at ![]() confirms the results found in step 6 on the concavity of
confirms the results found in step 6 on the concavity of ![]()
Combining this information, we arrive at the graph of ![]() shown in the following graph.
shown in the following graph.

Sketch a graph of ![]()
Solution

Sketching a Rational Function
Sketch the graph of ![]()
Solution
Step 1. The function ![]() is defined as long as the denominator is not zero. Therefore, the domain is the set of all real numbers
is defined as long as the denominator is not zero. Therefore, the domain is the set of all real numbers ![]() except
except ![]()
Step 2. Find the intercepts. If ![]() then
then ![]() so 0 is an intercept. If
so 0 is an intercept. If ![]() then
then ![]() which implies
which implies ![]() Therefore,
Therefore, ![]() is the only intercept.
is the only intercept.
Step 3. Evaluate the limits at infinity. Since ![]() is a rational function, divide the numerator and denominator by the highest power in the denominator:
is a rational function, divide the numerator and denominator by the highest power in the denominator: ![]() We obtain
We obtain
Therefore, ![]() has a horizontal asymptote of
has a horizontal asymptote of ![]() as
as ![]() and
and ![]()
Step 4. To determine whether ![]() has any vertical asymptotes, first check to see whether the denominator has any zeroes. We find the denominator is zero when
has any vertical asymptotes, first check to see whether the denominator has any zeroes. We find the denominator is zero when ![]() To determine whether the lines
To determine whether the lines ![]() or
or ![]() are vertical asymptotes of
are vertical asymptotes of ![]() evaluate
evaluate ![]() and
and ![]() By looking at each one-sided limit as
By looking at each one-sided limit as ![]() we see that
we see that
In addition, by looking at each one-sided limit as ![]() we find that
we find that
Step 5. Calculate the first derivative:
Critical numbers occur at points ![]() where
where ![]() or
or ![]() is undefined. We see that
is undefined. We see that ![]() when
when ![]() The derivative
The derivative ![]() is not undefined at any point in the domain of
is not undefined at any point in the domain of ![]() However,
However, ![]() are not in the domain of
are not in the domain of ![]() Therefore, to determine where
Therefore, to determine where ![]() is increasing and where
is increasing and where ![]() is decreasing, divide the interval
is decreasing, divide the interval ![]() into four smaller intervals:
into four smaller intervals: ![]()
![]()
![]() and
and ![]() and choose a test point in each interval to determine the sign of
and choose a test point in each interval to determine the sign of ![]() in each of these intervals. The values
in each of these intervals. The values ![]()
![]()
![]() and
and ![]() are good choices for test points as shown in the following table.
are good choices for test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
From this analysis, we conclude that ![]() has a local minimum at
has a local minimum at ![]() but no local maximum.
but no local maximum.
Step 6. Calculate the second derivative:
![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill f''(x)& \hfill =\frac{{(1-{x}^{2})}^{2}(2)-2x(2(1-{x}^{2})(-2x))}{{(1-{x}^{2})}^{4}}\\ & =\frac{(1-{x}^{2})\left[2(1-{x}^{2})+8{x}^{2}\right]}{{(1-{x}^{2})}^{4}}\hfill \\ & =\frac{2(1-{x}^{2})+8{x}^{2}}{{(1-{x}^{2})}^{3}}\hfill \\ & =\frac{6{x}^{2}+2}{{(1-{x}^{2})}^{3}}.\hfill \end{array}](https://opentextbooks.clemson.edu/app/uploads/quicklatex/quicklatex.com-4620068b3612c746b8a5f42b5c4dcfec_l3.png)
To determine the intervals where ![]() is concave up and where
is concave up and where ![]() is concave down, we first need to find all points
is concave down, we first need to find all points ![]() where
where ![]() or
or ![]() is undefined. Since the numerator
is undefined. Since the numerator ![]() for any
for any ![]()
![]() is never zero. Furthermore,
is never zero. Furthermore, ![]() is not undefined for any
is not undefined for any ![]() in the domain of
in the domain of ![]() However, as discussed earlier,
However, as discussed earlier, ![]() are not in the domain of
are not in the domain of ![]() Therefore, to determine the concavity of
Therefore, to determine the concavity of ![]() we divide the interval
we divide the interval ![]() into the three smaller intervals
into the three smaller intervals ![]()
![]() and
and ![]() and choose a test point in each of these intervals to evaluate the sign of
and choose a test point in each of these intervals to evaluate the sign of ![]() in each of these intervals. The values
in each of these intervals. The values ![]()
![]() and
and ![]() are possible test points as shown in the following table.
are possible test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
Combining all this information, we arrive at the graph of ![]() shown below. Note that, although
shown below. Note that, although ![]() changes concavity at
changes concavity at ![]() and
and ![]() there are no inflection points at either of these places because
there are no inflection points at either of these places because ![]() is not continuous at
is not continuous at ![]() or
or ![]()

Sketch a graph of ![]()
Hint
A line ![]() is a horizontal asymptote of
is a horizontal asymptote of ![]() if the limit as
if the limit as ![]() or the limit as
or the limit as ![]() of
of ![]() is
is ![]() A line
A line ![]() is a vertical asymptote if at least one of the one-sided limits of
is a vertical asymptote if at least one of the one-sided limits of ![]() as
as ![]() is
is ![]() or
or ![]()
Solution

Sketching a Rational Function with an Oblique Asymptote
Sketch the graph of ![]()
Solution
Step 1. The domain of ![]() is the set of all real numbers
is the set of all real numbers ![]() except
except ![]()
Step 2. Find the intercepts. We can see that when ![]()
![]() so
so ![]() is the only intercept.
is the only intercept.
Step 3. Evaluate the limits at infinity. Since the degree of the numerator is one more than the degree of the denominator, ![]() must have an oblique asymptote. To find the oblique asymptote, use long division of polynomials to write
must have an oblique asymptote. To find the oblique asymptote, use long division of polynomials to write
Since ![]() as
as ![]()
![]() approaches the line
approaches the line ![]() as
as ![]() The line
The line ![]() is an oblique asymptote for
is an oblique asymptote for ![]()
Step 4. To check for vertical asymptotes, look at where the denominator is zero. Here the denominator is zero at ![]() Looking at both one-sided limits as
Looking at both one-sided limits as ![]() we find
we find
Therefore, ![]() is a vertical asymptote, and we have determined the behavior of
is a vertical asymptote, and we have determined the behavior of ![]() as
as ![]() approaches 1 from the right and the left.
approaches 1 from the right and the left.
Step 5. Calculate the first derivative:
We have ![]() when
when ![]() Therefore,
Therefore, ![]() and
and ![]() are critical numbers. Since
are critical numbers. Since ![]() is undefined at
is undefined at ![]() we need to divide the interval
we need to divide the interval ![]() into the smaller intervals
into the smaller intervals ![]()
![]()
![]() and
and ![]() and choose a test point from each interval to evaluate the sign of
and choose a test point from each interval to evaluate the sign of ![]() in each of these smaller intervals. For example, let
in each of these smaller intervals. For example, let ![]()
![]()
![]() and
and ![]() be the test points as shown in the following table.
be the test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
From this table, we see that ![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() The value of
The value of ![]() at the local maximum is
at the local maximum is ![]() and the value of
and the value of ![]() at the local minimum is
at the local minimum is ![]() Therefore,
Therefore, ![]() and
and ![]() are important points on the graph.
are important points on the graph.
Step 6. Calculate the second derivative:
![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill f''(x)& =\frac{{(x-1)}^{2}(2x-2)-({x}^{2}-2x)(2(x-1))}{{(x-1)}^{4}}\hfill \\ & =\frac{(x-1)\left[(x-1)(2x-2)-2({x}^{2}-2x)\right]}{{(x-1)}^{4}}\hfill \\ & =\frac{(x-1)(2x-2)-2({x}^{2}-2x)}{{(x-1)}^{3}}\hfill \\ & =\frac{2{x}^{2}-4x+2-(2{x}^{2}-4x)}{{(x-1)}^{3}}\hfill \\ & =\frac{2}{{(x-1)}^{3}}.\hfill \end{array}](https://opentextbooks.clemson.edu/app/uploads/quicklatex/quicklatex.com-bb35add52a6da9bbed27defa16e8ffaa_l3.png)
We see that ![]() is never zero or undefined for
is never zero or undefined for ![]() in the domain of
in the domain of ![]() Since
Since ![]() is undefined at
is undefined at ![]() to check concavity we just divide the interval
to check concavity we just divide the interval ![]() into the two smaller intervals
into the two smaller intervals ![]() and
and ![]() and choose a test point from each interval to evaluate the sign of
and choose a test point from each interval to evaluate the sign of ![]() in each of these intervals. The values
in each of these intervals. The values ![]() and
and ![]() are possible test points as shown in the following table.
are possible test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
From the information gathered, we arrive at the following graph for ![]()

Find the oblique asymptote for ![]()
Hint
Use long division of polynomials.
Solution
![]()
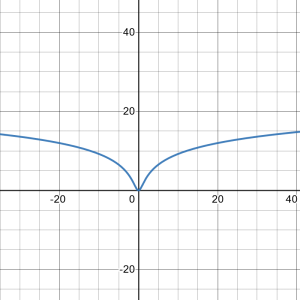
Sketching the Graph of a Function with a Cusp
Sketch a graph of ![]()
Solution
Step 1. Since the cube-root function is defined for all real numbers ![]() and
and ![]() the domain of
the domain of ![]() is all real numbers.
is all real numbers.
Step 2: To find the ![]() -intercept, evaluate
-intercept, evaluate ![]() Since
Since ![]() the
the ![]() -intercept is
-intercept is ![]() To find the
To find the ![]() -intercept, solve
-intercept, solve ![]() The solution of this equation is
The solution of this equation is ![]() so the
so the ![]() -intercept is
-intercept is ![]()
Step 3: Since ![]() the function continues to grow without bound as
the function continues to grow without bound as ![]() and
and ![]()
Step 4: The function has no vertical asymptotes.
Step 5: To determine where ![]() is increasing or decreasing, calculate
is increasing or decreasing, calculate ![]() We find
We find
This function is not zero anywhere, but it is undefined when ![]() Therefore, the only critical number is
Therefore, the only critical number is ![]() Divide the interval
Divide the interval ![]() into the smaller intervals
into the smaller intervals ![]() and
and ![]() and choose test points in each of these intervals to determine the sign of
and choose test points in each of these intervals to determine the sign of ![]() in each of these smaller intervals. Let
in each of these smaller intervals. Let ![]() and
and ![]() be the test points as shown in the following table.
be the test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
We conclude that ![]() has a local minimum at
has a local minimum at ![]() Evaluating
Evaluating ![]() at
at ![]() we find that the value of
we find that the value of ![]() at the local minimum is zero. Note that
at the local minimum is zero. Note that ![]() is undefined, so to determine the behavior of the function at this critical number, we need to examine
is undefined, so to determine the behavior of the function at this critical number, we need to examine ![]() Looking at the one-sided limits, we have
Looking at the one-sided limits, we have
Therefore, ![]() has a cusp at
has a cusp at ![]()
Step 6: To determine concavity, we calculate the second derivative of ![]()
We find that ![]() is defined for all
is defined for all ![]() but is undefined when
but is undefined when ![]() Therefore, divide the interval
Therefore, divide the interval ![]() into the smaller intervals
into the smaller intervals ![]() and
and ![]() and choose test points to evaluate the sign of
and choose test points to evaluate the sign of ![]() in each of these intervals. As we did earlier, let
in each of these intervals. As we did earlier, let ![]() and
and ![]() be test points as shown in the following table.
be test points as shown in the following table.
| Interval | Test Point | Sign of |
Conclusion |
|---|---|---|---|
From this table, we conclude that ![]() is concave down everywhere. Combining all of this information, we arrive at the following graph for
is concave down everywhere. Combining all of this information, we arrive at the following graph for ![]()

Consider the function ![]() Determine the point on the graph where a cusp is located. Determine the end behavior of
Determine the point on the graph where a cusp is located. Determine the end behavior of ![]()
Hint
A function ![]() has a cusp at a point
has a cusp at a point ![]() if
if ![]() exists,
exists, ![]() is undefined, one of the one-sided limits as
is undefined, one of the one-sided limits as ![]() of
of ![]() is
is ![]() and the other one-sided limit is
and the other one-sided limit is ![]()
Solution
The function ![]() has a cusp at
has a cusp at ![]()
![]()
![]() For end behavior,
For end behavior, ![]()
For the following exercises, sketch the function by finding the following:
- Determine the domain of the function.
- Determine the
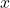 – and
– and 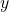 -intercepts.
-intercepts. - Determine any horizontal or vertical asymptotes.
- Determine the intervals where the function is increasing and where the function is decreasing. Determine whether the function has any local extrema.
- Determine the intervals where the function is concave up and where the function is concave down.
- Determine all inflection points (if any).
1. ![]()
2. ![]()
Solution

3. ![]()
4. ![]()
Solution

5. ![]()
6. ![]()
Solution

7. ![]()
8. ![]() on
on ![]()
Solution

9. ![]()
10. ![]()
Solution

11. ![]()
12. ![]()
Solution

13. ![]()
For the following exercises, sketch the graph of ![]() by finding the following:
by finding the following:
- Determine the domain of the function.
- Determine the
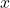 – and
– and 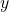 -intercepts.
-intercepts. - Determine any horizontal or vertical asymptotes.
- Determine the intervals where
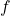 is increasing and where
is increasing and where 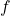 is decreasing. Determine whether
is decreasing. Determine whether 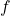 has any local extrema.
has any local extrema. - Determine the intervals where
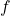 is concave up and where
is concave up and where 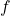 is concave down.
is concave down. - Determine all inflection points (if any).
14. ![]()
Solution
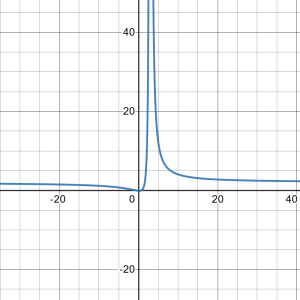
15. ![]()
16. ![]()
Solution
17. ![]()

