7

True or False ? Justify your answer with a proof or a counterexample.

1.  A function is always one-to-one.

2.  f \circ g=g\circ f, assuming f and g are functions.

Solution

False

3.  A relation that passes the horizontal and vertical line tests is a one-to-one function.

4.  A relation passing the horizontal line test is a function.

Solution

False

For the following problems, state the domain and range of the given functions:

f=x^2+2x-3,\phantom{\rule{3em}{0ex}}g=\ln(x-5),\phantom{\rule{3em}{0ex}}h=\frac{1}{x+4}

5.  h

6.  g

Solution

Domain: (5,\infty), Range: all real numbers

7.  h\circ f

8.  g\circ f

Solution

Domain: (-\infty,-4) \cup (2,\infty), Range: all real numbers

Given the following functions, determine: f(2), f(a) and f(a+h)

9. f(x)=\frac{5}{2x-3}

10. f(x)=\frac{x}{x-1}

Solution

f(2) = 2, f(a) = \frac{a}{a-1}, f(a+h) = \frac{a+h}{a+h-1}

11. f(x)=\sqrt{7-x}

12. f(x)=\frac{x^2-1}{x-2}

Solution

f(2) does not exist since 2 is not in the domain of f, f(a) = \frac{a^2-1}{a-2}, f(a+h) = \frac{(a+h)^2-1}{a+h-2} = \frac{a^2 + 2ah + h^2 -1}{a+h-2}

Determine the domain of each function. Write your answer in interval notation.

13. f(x)=\frac{x+5}{\sqrt{x^2+5x-14}}

14.f(x)=\frac{x-2}{\sqrt{x^2-3x+2}}

Solution

Domain: (-\infty,1) \cup (2,\infty)

15. f(x)=\sqrt{5x-1} - \sqrt{x}

16. f(x)=\sqrt{3x} - \sqrt{2-x}

Solution

Domain: [0,2]

17. f(x)=\frac{x^2+3}{\sqrt{x^2-9}}

18. f(x)=\frac{x^2+3}{\sqrt{9-x^2}}

Solution

Domain: (-3,3)

19. f(x)=e^{x^2+x-2}

20. f(x)= \frac{x}{1-e^{3x^2-4x-7}}

Solution

Domain: (-\infty,-1) \cup (-1, \frac{7}{3}) \cup (\frac{7}{3},\infty)

21. f(x)= \ln(16-x^2)

22. f(x)= \ln(2x^2-50)

Solution

Domain: (-\infty,-5) \cup (5,\infty)

23. f(x)= \frac{4x}{|x^2-36|}

24. f(x)= \frac{\sqrt{x-7}}{|x^2-49|}

Solution

Domain: (7,\infty)

25. f(x)= \frac{\sqrt{9-x}}{x^2-5x-24}

26. f(x)= \frac{\sqrt{x^2-6x+8}}{16-x^2}

Solution

Domain: (-\infty,-4) \cup (-4,2] \cup (4,\infty)

27. g(x) =\frac{\sqrt{4-x}}{x^2+3x+2}

28. h(x)=\dfrac{\sqrt{1-e^x}}{x+6}

Solution

Domain: (-\infty,-6)\cup(-6,0]

Find the inverse of the following functions.

29. f(x)=\frac{2x-1}{7}

30. g(x)=\frac{x-8}{2x+1}

Solution

g^{-1}(x)= \frac{-x-8}{2x-1}

31. g(x)=\ln(x-7)

32. f(x)=e^{2x}-3

Solution

f^{-1}(x)= \frac{lnx+3}{2}

Find the degree, y-intercept, and zeros for the following polynomial functions.

33.  f(x)=2x^2+9x-5

34.  f(x)=x^3+2x^2-2x

Solution

Degree of 3, y-intercept: 0, Zeros: 0, \sqrt{3}-1, \, -1-\sqrt{3}

Simplify the following trigonometric expressions.

35.  \frac{\tan^2 x}{\sec^2 x}+\cos^2 x

36.  \cos(2x)=\sin^2 x

Solution

\cos(2x) or \frac{1}{2}(\cos(2x)+1)

Solve the following trigonometric equations on the interval \theta =[-2\pi ,2\pi] exactly.

37.  6\cos^2 x-3=0

38.  \sec^2 x-2\sec x+1=0

Solution

0, \, \pm 2\pi

Solve the following logarithmic equations.

39.  5^x=16

40.  \log_2 (x+4)=3

Solution

4

Are the following functions one-to-one over their domain of existence? Does the function have an inverse? If so, find the inverse f^{-1}(x) of the function. Justify your answer.

41.  f(x)=x^2+2x+1

42.  f(x)=\frac{1}{x}

Solution

One-to-one; yes, the function has an inverse; inverse: f^{-1}(x)=\frac{1}{x}

For the following problems, determine the largest domain on which the function is one-to-one and find the inverse on that domain.

43.  f(x)=\sqrt{9-x}

44.  f(x)=x^2+3x+4

Solution

x \ge -\frac{3}{2}, \, f^{-1}(x)=-\frac{3}{2}+\frac{1}{2}\sqrt{4y-7}

Sketch the following piece-wise functions.

45. f(x)=\begin{cases} x+7, & x < 1 \\ x-5 & x \ge 1 \end{cases}

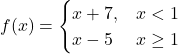
46. f(x)=\begin{cases} x^2-1, & x < -2 \\ x+2 & x \ge -2 \end{cases}

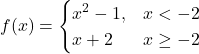
Solution

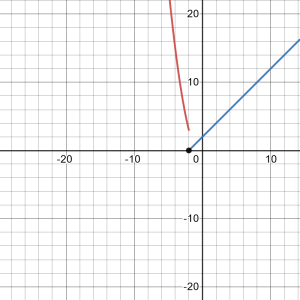
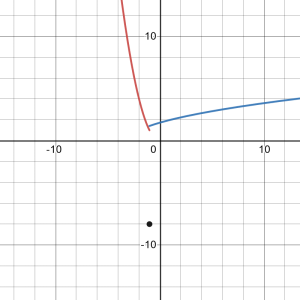
47. f(x)=\begin{cases} x-1, & x < 1 \\ 4, & x=1 \\ \sqrt{x+2} & x > 1 \end{cases}

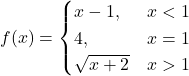
48. f(x)=\begin{cases} x^2, & x < -1 \\ x-7, & x=-1 \\ \sqrt{x+3} & x > -1 \end{cases}

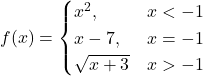
Solution

Write the following absolute value functions as piece-wise functions and sketch.

49. f(x)=|2x-5|

50. f(x)=|3x+7|

Solution

f(x)=\begin{cases} -(3x+7), & x < -\frac{7}{3} \\ 3x+7 & x \ge -\frac{7}{3} \end{cases}

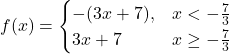
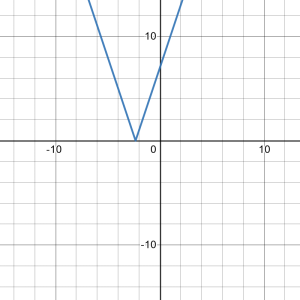
Answer the following question.

51.  A car is racing along a circular track with diameter of 1 mi. A trainer standing in the center of the circle marks his progress every 5 sec. After 5 sec, the trainer has to turn 55^{\circ} to keep up with the car. How fast is the car traveling?

For the following problems, consider a restaurant owner who wants to sell T-shirts advertising his brand. He recalls that there is a fixed cost and variable cost, although he does not remember the values. He does know that the T-shirt printing company charges $440 for 20 shirts and $1000 for 100 shirts.

52.  a. Find the equation C=f(x) that describes the total cost as a function of number of shirts and b. determine how many shirts he must sell to break even if he sells the shirts for $10 each.

Solution

a. C(x)=300+7x b. 100 shirts

53.  a. Find the inverse function x=f^{-1}(C) and describe the meaning of this function. b. Determine how many shirts the owner can buy if he has $8000 to spend.

For the following problems, consider the population of Ocean City, New Jersey, which is cyclical by season.

54.  The population can be modeled by P(t)=82.5-67.5\cos [(\pi /6)t], where t is time in months (t=0 represents January 1) and P is population (in thousands). During a year, in what intervals is the population less than 20,000? During what intervals is the population more than 140,000?

Solution

The population is less than 20,000 from December 8 through January 23 and more than 140,000 from May 29 through August 2

55.  In reality, the overall population is most likely increasing or decreasing throughout each year. Let’s reformulate the model as P(t)=82.5-67.5\cos [(\pi /6)t]+t, where t is time in months (t=0 represents January 1) and P is population (in thousands). When is the first time the population reaches 200,000?

For the following problems, consider radioactive dating. A human skeleton is found in an archeological dig. Carbon dating is implemented to determine how old the skeleton is by using the equation y=e^{rt}, where y is the percentage of radiocarbon still present in the material, t is the number of years passed, and r=-0.0001210 is the decay rate of radiocarbon.

56.  If the skeleton is expected to be 2000 years old, what percentage of radiocarbon should be present?

Solution

78.51%

57.  Find the inverse of the carbon-dating equation. What does it mean? If there is 25% radiocarbon, how old is the skeleton?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Calculus Volume 1 Copyright © 2016 by OSCRiceUniversity is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book