40
Learning Objectives
- Integrate functions involving exponential functions.
- Integrate functions involving logarithmic functions.
Exponential and logarithmic functions are used to model population growth, cell growth, and financial growth, as well as depreciation, radioactive decay, and resource consumption, to name only a few applications. In this section, we explore integration involving exponential and logarithmic functions.
Integrals of Exponential Functions
The exponential function is perhaps the most efficient function in terms of the operations of calculus. The exponential function, ![]() is its own derivative and its own integral.
is its own derivative and its own integral.
Rule: Integrals of Exponential Functions
Exponential functions can be integrated using the following formulas.
Finding an Antiderivative of an Exponential Function
Find the antiderivative of the exponential function ![]() –
–![]() .
.
Solution
Use substitution, setting ![]() and then
and then ![]() Multiply the du equation by -1, so you now have
Multiply the du equation by -1, so you now have ![]() Then,
Then,
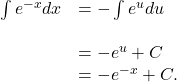
Find the antiderivative of the function using substitution: ![]()
Solution
![]()
A common mistake when dealing with exponential expressions is treating the exponent on ![]() the same way we treat exponents in polynomial expressions. We cannot use the power rule for the exponent on
the same way we treat exponents in polynomial expressions. We cannot use the power rule for the exponent on ![]() . This can be especially confusing when we have both exponentials and polynomials in the same expression, as in the previous checkpoint. In these cases, we should always double-check to make sure we’re using the right rules for the functions we’re integrating.
. This can be especially confusing when we have both exponentials and polynomials in the same expression, as in the previous checkpoint. In these cases, we should always double-check to make sure we’re using the right rules for the functions we’re integrating.
Square Root of an Exponential Function
Find the antiderivative of the exponential function ![]()
Solution
First rewrite the problem using a rational exponent:
Using substitution, choose ![]() Then,
Then, ![]() We have ( (Figure) )
We have ( (Figure) )
Then
![A graph of the function f(x) = e^x * sqrt(1 + e^x), which is an increasing concave up curve, over [-3, 1]. It begins close to the x axis in quadrant two, crosses the y axis at (0, sqrt(2)), and continues to increase rapidly.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11204252/CNX_Calc_Figure_05_06_001.jpg)
Find the antiderivative of ![]()
![]()
Hint
Let ![]()
Using Substitution with an Exponential Function
Solution
Here we choose to let ![]() equal the expression in the exponent on
equal the expression in the exponent on ![]() . Let
. Let ![]() and
and ![]() Again, du is off by a constant multiplier; the original function contains a factor of 3
Again, du is off by a constant multiplier; the original function contains a factor of 3![]() 2 , not 6
2 , not 6![]() 2 . Multiply both sides of the equation by
2 . Multiply both sides of the equation by ![]() so that the integrand in
so that the integrand in ![]() equals the integrand in
equals the integrand in ![]() . Thus,
. Thus,
Integrate the expression in ![]() and then substitute the original expression in
and then substitute the original expression in ![]() back into the
back into the ![]() integral:
integral:
Evaluate the indefinite integral ![]()
Solution
![]()
Hint
Let ![]()
As mentioned at the beginning of this section, exponential functions are used in many real-life applications. The number ![]() is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth. Let’s look at an example in which integration of an exponential function solves a common business application.
is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth. Let’s look at an example in which integration of an exponential function solves a common business application.
A price–demand function tells us the relationship between the quantity of a product demanded and the price of the product. In general, price decreases as quantity demanded increases. The marginal price–demand function is the derivative of the price–demand function and it tells us how fast the price changes at a given level of production. These functions are used in business to determine the price–elasticity of demand, and to help companies determine whether changing production levels would be profitable.
Finding a Price–Demand Equation
Find the price–demand equation for a particular brand of toothpaste at a supermarket chain when the demand is 50 tubes per week at $2.35 per tube, given that the marginal price—demand function, ![]() for
for ![]() number of tubes per week, is given as
number of tubes per week, is given as
If the supermarket chain sells 100 tubes per week, what price should it set?
Solution
To find the price–demand equation, integrate the marginal price–demand function. First find the antiderivative, then look at the particulars. Thus,
Using substitution, let ![]() and
and ![]() Then, divide both sides of the du equation by -0.01. This gives
Then, divide both sides of the du equation by -0.01. This gives
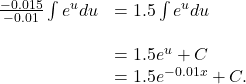
The next step is to solve for C . We know that when the price is $2.35 per tube, the demand is 50 tubes per week. This means
Now, just solve for C :
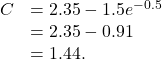
Thus,
If the supermarket sells 100 tubes of toothpaste per week, the price would be
The supermarket should charge $1.99 per tube if it is selling 100 tubes per week.
Evaluating a Definite Integral Involving an Exponential Function
Evaluate the definite integral ![]()
Solution
Again, substitution is the method to use. Let ![]() so
so ![]() or
or ![]() Then
Then ![]() Next, change the limits of integration. Using the equation
Next, change the limits of integration. Using the equation ![]() we have
we have
The integral then becomes
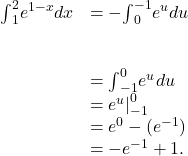
See (Figure) .
![A graph of the function f(x) = e^(1-x) over [0, 3]. It crosses the y axis at (0, e) as a decreasing concave up curve and symptotically approaches 0 as x goes to infinity.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11204254/CNX_Calc_Figure_05_06_002.jpg)
Evaluate ![]()
Solution
![]()
Hint
Let ![]()
Growth of Bacteria in a Culture
Suppose the rate of growth of bacteria in a Petri dish is given by ![]() where
where ![]() is given in hours and
is given in hours and ![]() is given in thousands of bacteria per hour. If a culture starts with 10,000 bacteria, find a function
is given in thousands of bacteria per hour. If a culture starts with 10,000 bacteria, find a function ![]() that gives the number of bacteria in the Petri dish at any time
that gives the number of bacteria in the Petri dish at any time ![]() . How many bacteria are in the dish after 2 hours?
. How many bacteria are in the dish after 2 hours?
Solution
We have
Then, at ![]() we have
we have ![]() so
so ![]() and we get
and we get
At time ![]() we have
we have
After 2 hours, there are 17,282 bacteria in the dish.
Fruit Fly Population Growth
Suppose a population of fruit flies increases at a rate of ![]() in flies per day. If the initial population of fruit flies is 100 flies, how many flies are in the population after 10 days?
in flies per day. If the initial population of fruit flies is 100 flies, how many flies are in the population after 10 days?
Solution
Let ![]() represent the number of flies in the population at time
represent the number of flies in the population at time ![]() . Applying the net change theorem, we have
. Applying the net change theorem, we have
![Rendered by QuickLaTeX.com \begin{array}{cc}\\ \\ G(10)\hfill & =G(0)+{\int }_{0}^{10}2{e}^{0.02t}dt\hfill \\ & =100+{\left[\frac{2}{0.02}{e}^{0.02t}\right]|}_{0}^{10}\hfill \\ & =100+{\left[100{e}^{0.02t}\right]|}_{0}^{10}\hfill \\ & =100+100{e}^{0.2}-100\hfill \\ & \approx 122.\hfill \end{array}](https://opentextbooks.clemson.edu/app/uploads/quicklatex/quicklatex.com-7917228ee49fadb7df0a2b194d81320d_l3.png)
There are 122 flies in the population after 10 days.
Suppose the rate of growth of the fly population is given by ![]() and the initial fly population is 100 flies. How many flies are in the population after 15 days?
and the initial fly population is 100 flies. How many flies are in the population after 15 days?
Solution
There are 116 flies.
Hint
Use the process from (Figure) to solve the problem.
Evaluating a Definite Integral Using Substitution
Evaluate the definite integral using substitution: ![]()
Solution
This problem requires some rewriting to simplify applying the properties. First, rewrite the exponent on ![]() as a power of
as a power of ![]() , then bring the
, then bring the ![]() 2 in the denominator up to the numerator using a negative exponent. We have
2 in the denominator up to the numerator using a negative exponent. We have
Let ![]() the exponent on
the exponent on ![]() . Then
. Then
Bringing the negative sign outside the integral sign, the problem now reads
Next, change the limits of integration:
Notice that now the limits begin with the larger number, meaning we must multiply by -1 and interchange the limits. Thus,
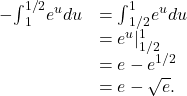
Evaluate the definite integral using substitution: ![]()
Solution
![]()
Hint
Let ![]()
Integrals Involving Logarithmic Functions
Integrating functions of the form ![]() result in the absolute value of the natural log function, as shown in the following rule. Integral formulas for other logarithmic functions, such as
result in the absolute value of the natural log function, as shown in the following rule. Integral formulas for other logarithmic functions, such as ![]() and
and ![]() are also included in the rule.
are also included in the rule.
Rule: Integration Formulas Involving Logarithmic Functions
The following formulas can be used to evaluate integrals involving logarithmic functions.
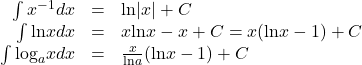
Finding an Antiderivative Involving 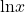
Find the antiderivative of the function ![]()
Solution
First factor the 3 outside the integral symbol. Then use the ![]() -1 rule. Thus,
-1 rule. Thus,
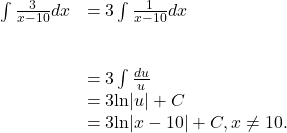
See (Figure) .
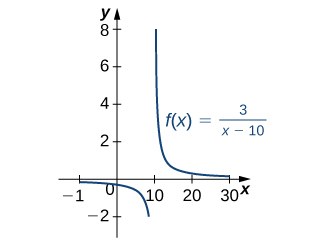
Finding an Antiderivative of a Rational Function
Find the antiderivative of ![]()
This can be rewritten as ![]() Use substitution. Let
Use substitution. Let ![]() then
then ![]() Alter du by factoring out the 2. Thus,
Alter du by factoring out the 2. Thus,
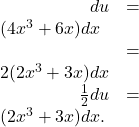
Rewrite the integrand in ![]() :
:
Then we have
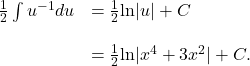
Finding an Antiderivative of a Logarithmic Function
Find the antiderivative of the log function ![]()
Solution
Follow the format in the formula listed in the rule on integration formulas involving logarithmic functions. Based on this format, we have
Find the antiderivative of ![]()
Solution
![]()
Hint
Follow (Figure) and refer to the rule on integration formulas involving logarithmic functions.
(Figure) is a definite integral of a trigonometric function. With trigonometric functions, we often have to apply a trigonometric property or an identity before we can move forward. Finding the right form of the integrand is usually the key to a smooth integration.
Evaluating a Definite Integral
Find the definite integral of ![]()
Solution
We need substitution to evaluate this problem. Let ![]() so
so ![]() Rewrite the integral in terms of
Rewrite the integral in terms of ![]() , changing the limits of integration as well. Thus,
, changing the limits of integration as well. Thus,
Then
![Rendered by QuickLaTeX.com \begin{array}{cc}{\int }_{0}^{\pi \text{/}2}\frac{ \sin x}{1+ \cos x}\hfill & =-{\int }_{2}^{1}{u}^{-1}du\hfill \\ \\ \\ & ={\int }_{1}^{2}{u}^{-1}du\hfill \\ & ={\text{ln}|u||}_{1}^{2}\hfill \\ & =\left[\text{ln}2-\text{ln}1\right]\hfill \\ & =\text{ln}2.\hfill \end{array}](https://opentextbooks.clemson.edu/app/uploads/quicklatex/quicklatex.com-2936c6013f299a3d0cb54213e752aaad_l3.png)
Key Concepts
- Exponential and logarithmic functions arise in many real-world applications, especially those involving growth and decay.
- Substitution is often used to evaluate integrals involving exponential functions or logarithms.
Key Equations
- Integrals of Exponential Functions
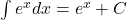
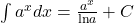
- Integration Formulas Involving Logarithmic Functions
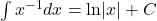
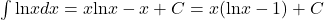
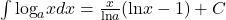
In the following exercises, compute each indefinite integral.
1. ![]()
2. ![]()
Solution
![]()
3. ![]()
4. ![]()
Solution
![]()
5. ![]()
6. ![]()
Solution
![]()
7. ![]()
8. ![]()
Solution
![]()
In the following exercises, find each indefinite integral by using appropriate substitutions.
9. ![]()
10. ![]()
Solution
![]()
11. ![]()
12. ![]()
Solution
![]()
13. ![]()
14. ![]()
Solution
![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
Solution
![]()
19. ![]()
20. ![]()
Solution
![]()
21. ![]()
22. ![]()
Solution
![]()
In the following exercises, verify by differentiation that ![]() then use appropriate changes of variables to compute the integral.
then use appropriate changes of variables to compute the integral.
23. ![]() [latex](Hint\text{:}\int \text{ln}xdx=\frac{1}{2}\int x\text{ln}({x}^{2})dx)[/latex]
[latex](Hint\text{:}\int \text{ln}xdx=\frac{1}{2}\int x\text{ln}({x}^{2})dx)[/latex]
24. ![]()
Solution
![]()
25. ![]() [latex](Hint\text{:}\text{Set}u=\frac{1}{x}\text{.})[/latex]
[latex](Hint\text{:}\text{Set}u=\frac{1}{x}\text{.})[/latex]
26. ![]() [latex](Hint\text{:}\text{Set}u=\sqrt{x}\text{.})[/latex]
[latex](Hint\text{:}\text{Set}u=\sqrt{x}\text{.})[/latex]
Solution
![]()
27. Write an integral to express the area under the graph of ![]() from
from ![]() to e x and evaluate the integral.
to e x and evaluate the integral.
28. Write an integral to express the area under the graph of ![]() between
between ![]() and
and ![]() and evaluate the integral.
and evaluate the integral.
Solution
![]()
In the following exercises, use appropriate substitutions to express the trigonometric integrals in terms of compositions with logarithms.
29. ![]()
30. ![]()
Solution
![]()
31. ![]()
32. ![]()
Solution
![]()
33. ![]()
34. ![]()
Solution
![]()
35. ![]()
In the following exercises, evaluate the definite integral.
36. ![]()
Solution
![]()
37. ![]()
38. ![]()
Solution
![]()
39. ![]()
40. ![]()
Solution
![]()
In the following exercises, integrate using the indicated substitution.
41. ![]()
42. ![]()
Solution
![]()
43. ![]()
44. ![]()
Solution
![]()
45. ![]()
46. ![]()
Solution
![]()
In the following exercises, does the right-endpoint approximation overestimate or underestimate the exact area? Calculate the right endpoint estimate R 50 and solve for the exact area.
47. [T] ![]() over
over ![]()
48. [T] ![]() over
over ![]()
Solution
Exact solution: ![]() Since
Since ![]() is decreasing, the right endpoint estimate underestimates the area.
is decreasing, the right endpoint estimate underestimates the area.
49. [T] ![]() over
over ![]()
50. [T] ![]() over
over ![]()
Solution
Exact solution: ![]() Since
Since ![]() is increasing, the right endpoint estimate overestimates the area.
is increasing, the right endpoint estimate overestimates the area.
51. [T] ![]() over
over ![]()
52. [T] ![]() over
over ![]()
Solution
Exact solution: ![]() Since
Since ![]() is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).
is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).
In the following exercises, ![]() for
for ![]() Find the area under the graph of
Find the area under the graph of ![]() between the given values
between the given values ![]() and
and ![]() by integrating.
by integrating.
53. ![]()
54. ![]()
Solution
![]()
55. ![]()
56. ![]()
Solution
![]()
57. Find the area under the graph of the function ![]() between
between ![]() and
and ![]()
58. Compute the integral of ![]() and find the smallest value of N such that the area under the graph
and find the smallest value of N such that the area under the graph ![]() between
between ![]() and
and ![]() is, at most, 0.01.
is, at most, 0.01.
Solution
![]() The quantity is less than 0.01 when
The quantity is less than 0.01 when ![]()
59. Find the limit, as N tends to infinity, of the area under the graph of ![]() between
between ![]() and
and ![]()
60. Show that ![]() when
when ![]()
Solution
![]()
61. Suppose that ![]() for all
for all ![]() and that
and that ![]() and
and ![]() are differentiable. Use the identity
are differentiable. Use the identity ![]() and the chain rule to find the derivative of
and the chain rule to find the derivative of ![]()
62. Use the previous exercise to find the antiderivative of ![]() and evaluate
and evaluate ![]()
Solution
23
63. Show that if ![]() then the integral of
then the integral of ![]() from ac to bc
from ac to bc ![]() is the same as the integral of
is the same as the integral of ![]() from
from ![]() to
to ![]() .
.
The following exercises are intended to derive the fundamental properties of the natural log starting from the Definition ![]() using properties of the definite integral and making no further assumptions.
using properties of the definite integral and making no further assumptions.
64. Use the identity ![]() to derive the identity
to derive the identity ![]()
Solution
We may assume that ![]() Then,
Then, ![]() Now make the substitution
Now make the substitution ![]() so
so ![]() and
and ![]() and change endpoints:
and change endpoints: ![]()
65. Use a change of variable in the integral ![]() to show that
to show that ![]()
66. Use the identity ![]() to show that
to show that ![]() is an increasing function of
is an increasing function of ![]() on
on ![]() and use the previous exercises to show that the range of
and use the previous exercises to show that the range of ![]() is
is ![]() Without any further assumptions, conclude that
Without any further assumptions, conclude that ![]() has an inverse function defined on
has an inverse function defined on ![]()
67. Pretend, for the moment, that we do not know that ![]() is the inverse function of
is the inverse function of ![]() but keep in mind that
but keep in mind that ![]() has an inverse function defined on
has an inverse function defined on ![]() Call it E . Use the identity
Call it E . Use the identity ![]() to deduce that
to deduce that ![]() for any real numbers
for any real numbers ![]() ,
, ![]() .
.
68. Pretend, for the moment, that we do not know that ![]() is the inverse function of
is the inverse function of ![]() but keep in mind that
but keep in mind that ![]() has an inverse function defined on
has an inverse function defined on ![]() Call it E . Show that
Call it E . Show that ![]()
Solution
![]() Then,
Then, ![]() Since any number
Since any number ![]() can be written
can be written ![]() for some
for some ![]() , and for such
, and for such ![]() we have
we have ![]() it follows that for any
it follows that for any ![]()
69. The sine integral, defined as ![]() is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large
is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large ![]() . Show that for
. Show that for ![]() (Hint:
(Hint: ![]() )
)
70. [T] The normal distribution in probability is given by ![]() where σ is the standard deviation and μ is the average. The standard normal distribution in probability,
where σ is the standard deviation and μ is the average. The standard normal distribution in probability, ![]() corresponds to
corresponds to ![]() Compute the left endpoint estimates
Compute the left endpoint estimates ![]() of
of ![]()
Solution
![]()
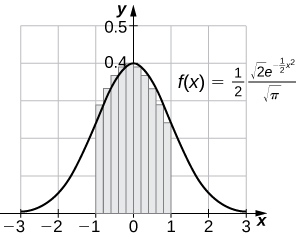
71. [T] Compute the right endpoint estimates ![]() of
of ![]()


Hint
Let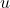 equal the exponent on
equal the exponent on  .
.