5
Learning Objectives
- Determine the conditions for when a function has an inverse.
- Use the horizontal line test to recognize when a function is one-to-one.
- Find the inverse of a given function.
- Draw the graph of an inverse function.
- Evaluate inverse trigonometric functions.
An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. In this section, we define an inverse function formally and state the necessary conditions for an inverse function to exist. We examine how to find an inverse function and study the relationship between the graph of a function and the graph of its inverse. Then we apply these ideas to define and discuss properties of the inverse trigonometric functions.
Existence of an Inverse Function
We begin with an example. Given a function ![]() and an output
and an output ![]() , we are often interested in finding what value or values
, we are often interested in finding what value or values ![]() were mapped to
were mapped to ![]() by
by ![]() . For example, consider the function
. For example, consider the function ![]() . Since any output
. Since any output ![]() , we can solve this equation for
, we can solve this equation for ![]() to find that the input is
to find that the input is ![]() . This equation defines
. This equation defines ![]() as a function of
as a function of ![]() . Denoting this function as
. Denoting this function as ![]() , and writing
, and writing ![]() , we see that for any
, we see that for any ![]() in the domain of
in the domain of ![]() . Thus, this new function,
. Thus, this new function, ![]() , “undid” what the original function
, “undid” what the original function ![]() did. A function with this property is called the inverse function of the original function.
did. A function with this property is called the inverse function of the original function.
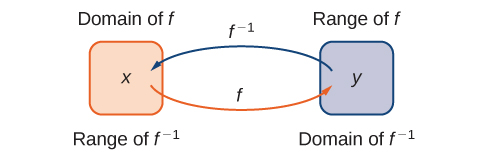
Definition
Given a function ![]() with domain
with domain ![]() and range
and range ![]() , its inverse function (if it exists) is the function
, its inverse function (if it exists) is the function ![]() with domain
with domain ![]() and range
and range ![]() such that
such that ![]() if
if ![]() . In other words, for a function
. In other words, for a function ![]() and its inverse
and its inverse ![]() ,
,
Note that ![]() is read as “f inverse.” Here, the -1 is not used as an exponent and
is read as “f inverse.” Here, the -1 is not used as an exponent and ![]() . (Figure) shows the relationship between the domain and range of
. (Figure) shows the relationship between the domain and range of ![]() and the domain and range of
and the domain and range of ![]() .
.
Recall that a function has exactly one output for each input. Therefore, to define an inverse function, we need to map each input to exactly one output. For example, let’s try to find the inverse function for ![]() . Solving the equation
. Solving the equation ![]() for
for ![]() , we arrive at the equation
, we arrive at the equation ![]() . This equation does not describe
. This equation does not describe ![]() as a function of
as a function of ![]() because there are two solutions to this equation for every
because there are two solutions to this equation for every ![]() . The problem with trying to find an inverse function for
. The problem with trying to find an inverse function for ![]() is that two inputs are sent to the same output for each output
is that two inputs are sent to the same output for each output ![]() . The function
. The function ![]() discussed earlier did not have this problem. For that function, each input was sent to a different output. A function that sends each input to a different output is called a one-to-one function.
discussed earlier did not have this problem. For that function, each input was sent to a different output. A function that sends each input to a different output is called a one-to-one function.
Definition
We say a ![]() is a one-to-one function if
is a one-to-one function if ![]() when
when ![]() .
.
One way to determine whether a function is one-to-one is by looking at its graph. If a function is one-to-one, then no two inputs can be sent to the same output. Therefore, if we draw a horizontal line anywhere in the ![]() -plane, according to the horizontal line test , it cannot intersect the graph more than once. We note that the horizontal line test is different from the vertical line test. The vertical line test determines whether a graph is the graph of a function. The horizontal line test determines whether a function is one-to-one ( (Figure) ).
-plane, according to the horizontal line test , it cannot intersect the graph more than once. We note that the horizontal line test is different from the vertical line test. The vertical line test determines whether a graph is the graph of a function. The horizontal line test determines whether a function is one-to-one ( (Figure) ).
Rule: Horizontal Line Test
A function ![]() is one-to-one if and only if every horizontal line intersects the graph of
is one-to-one if and only if every horizontal line intersects the graph of ![]() no more than once.
no more than once.
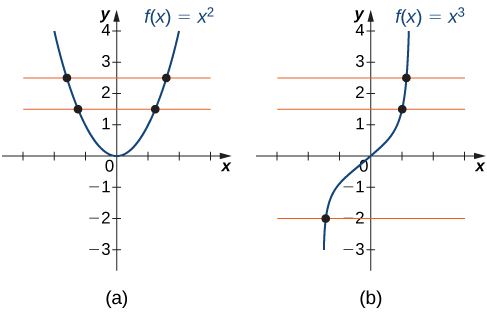
Determining Whether a Function Is One-to-One
For each of the following functions, use the horizontal line test to determine whether it is one-to-one.
Solution
- Since the horizontal line
 for any integer
for any integer  intersects the graph more than once, this function is not one-to-one.
intersects the graph more than once, this function is not one-to-one.

- Since every horizontal line intersects the graph once (at most), this function is one-to-one.

Is the function ![]() graphed in the following image one-to-one?
graphed in the following image one-to-one?
Hint
Use the horizontal line test.
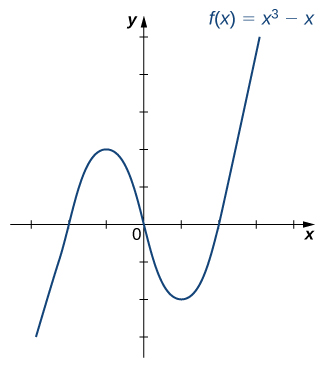
Solution
No.
Finding a Function’s Inverse
We can now consider one-to-one functions and show how to find their inverses. Recall that a function maps elements in the domain of ![]() to elements in the range of
to elements in the range of ![]() . The inverse function maps each element from the range of
. The inverse function maps each element from the range of ![]() back to its corresponding element from the domain of
back to its corresponding element from the domain of ![]() . Therefore, to find the inverse function of a one-to-one function
. Therefore, to find the inverse function of a one-to-one function ![]() , given any
, given any ![]() in the range of
in the range of ![]() , we need to determine which
, we need to determine which ![]() in the domain of
in the domain of ![]() satisfies
satisfies ![]() . Since
. Since ![]() is one-to-one, there is exactly one such value
is one-to-one, there is exactly one such value ![]() . We can find that value
. We can find that value ![]() by solving the equation
by solving the equation ![]() for
for ![]() . Doing so, we are able to write
. Doing so, we are able to write ![]() as a function of
as a function of ![]() where the domain of this function is the range of
where the domain of this function is the range of ![]() and the range of this new function is the domain of
and the range of this new function is the domain of ![]() . Consequently, this function is the inverse of
. Consequently, this function is the inverse of ![]() , and we write
, and we write ![]() . Since we typically use the variable
. Since we typically use the variable ![]() to denote the independent variable and
to denote the independent variable and ![]() to denote the dependent variable, we often interchange the roles of
to denote the dependent variable, we often interchange the roles of ![]() and
and ![]() , and write
, and write ![]() . Representing the inverse function in this way is also helpful later when we graph a function
. Representing the inverse function in this way is also helpful later when we graph a function ![]() and its inverse
and its inverse ![]() on the same axes.
on the same axes.
Problem-Solving Strategy: Finding an Inverse Function
- Solve the equation
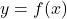 for
for 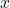 .
. - Interchange the variables
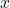 and
and 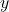 and write
and write 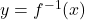 .
.
Finding an Inverse Function
Find the inverse for the function ![]() . State the domain and range of the inverse function. Verify that
. State the domain and range of the inverse function. Verify that ![]() .
.
Solution
Follow the steps outlined in the strategy.
Step 1. If ![]() , then
, then ![]() and
and ![]() .
.
Step 2. Rewrite as ![]() and let
and let ![]() .
.
Therefore, ![]() .
.
Since the domain of ![]() is
is ![]() , the range of
, the range of ![]() is
is ![]() . Since the range of
. Since the range of ![]() is
is ![]() , the domain of
, the domain of ![]() is
is ![]() .
.
You can verify that ![]() by writing
by writing
Note that for ![]() to be the inverse of
to be the inverse of ![]() , both
, both ![]() and
and ![]() for all
for all ![]() in the domain of the inside function.
in the domain of the inside function.
Find the inverse of the function ![]() . State the domain and range of the inverse function.
. State the domain and range of the inverse function.
Hint
Use the (Note) for finding inverse functions.
Solution
![]() . The domain of
. The domain of ![]() is
is ![]() . The range of
. The range of ![]() is
is ![]() .
.
Graphing Inverse Functions
Let’s consider the relationship between the graph of a function ![]() and the graph of its inverse. Consider the graph of
and the graph of its inverse. Consider the graph of ![]() shown in (Figure) and a point
shown in (Figure) and a point ![]() on the graph. Since
on the graph. Since ![]() , then
, then ![]() . Therefore, when we graph
. Therefore, when we graph ![]() , the point
, the point ![]() is on the graph. As a result, the graph of
is on the graph. As a result, the graph of ![]() is a reflection of the graph of
is a reflection of the graph of ![]() about the line
about the line ![]() .
.
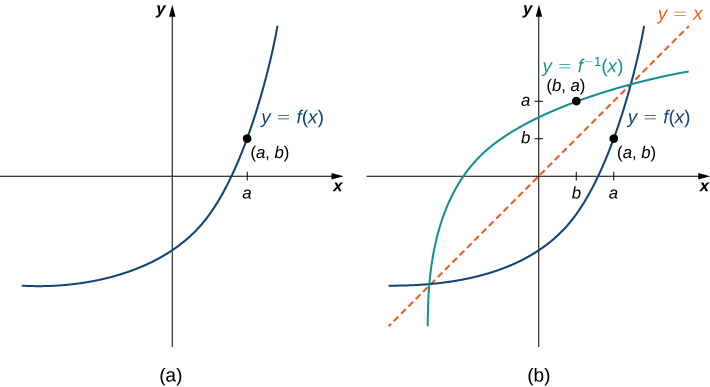
Sketching Graphs of Inverse Functions
For the graph of ![]() in the following image, sketch a graph of
in the following image, sketch a graph of ![]() by sketching the line
by sketching the line ![]() and using symmetry. Identify the domain and range of
and using symmetry. Identify the domain and range of ![]() .
.
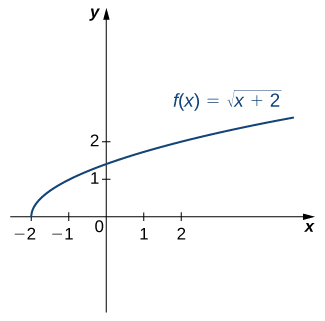
Solution
Reflect the graph about the line ![]() . The domain of
. The domain of ![]() is
is ![]() . The range of
. The range of ![]() is
is ![]() . By using the preceding strategy for finding inverse functions, we can verify that the inverse function is
. By using the preceding strategy for finding inverse functions, we can verify that the inverse function is ![]() , as shown in the graph.
, as shown in the graph.

Sketch the graph of ![]() and the graph of its inverse using the symmetry property of inverse functions.
and the graph of its inverse using the symmetry property of inverse functions.
Hint
The graphs are symmetric about the line ![]() .
.
Solution

Restricting Domains
As we have seen, ![]() does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of
does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of ![]() such that the function is one-to-one. This subset is called a restricted domain. By restricting the domain of
such that the function is one-to-one. This subset is called a restricted domain. By restricting the domain of ![]() , we can define a new function
, we can define a new function ![]() such that the domain of
such that the domain of ![]() is the restricted domain of
is the restricted domain of ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . Then we can define an inverse function for
. Then we can define an inverse function for ![]() on that domain. For example, since
on that domain. For example, since ![]() is one-to-one on the interval
is one-to-one on the interval ![]() , we can define a new function
, we can define a new function ![]() such that the domain of
such that the domain of ![]() is
is ![]() and
and ![]() for all
for all ![]() in its domain. Since
in its domain. Since ![]() is a one-to-one function, it has an inverse function, given by the formula
is a one-to-one function, it has an inverse function, given by the formula ![]() . On the other hand, the function
. On the other hand, the function ![]() is also one-to-one on the domain
is also one-to-one on the domain ![]() . Therefore, we could also define a new function
. Therefore, we could also define a new function ![]() such that the domain of
such that the domain of ![]() is
is ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . Then
. Then ![]() is a one-to-one function and must also have an inverse. Its inverse is given by the formula
is a one-to-one function and must also have an inverse. Its inverse is given by the formula ![]() ( (Figure) ).
( (Figure) ).
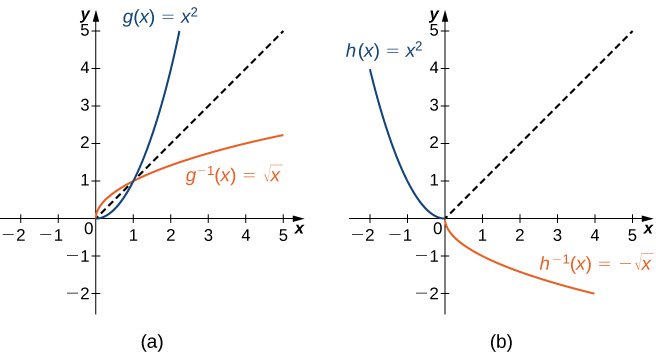
Restricting the Domain
Consider the function ![]() .
.
- Sketch the graph of
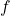 and use the horizontal line test to show that
and use the horizontal line test to show that 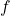 is not one-to-one.
is not one-to-one. - Show that
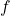 is one-to-one on the restricted domain
is one-to-one on the restricted domain 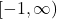 . Determine the domain and range for the inverse of
. Determine the domain and range for the inverse of 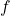 on this restricted domain and find a formula for
on this restricted domain and find a formula for 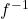 .
.
Solution
- The graph of
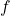 is the graph of
is the graph of 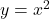 shifted left 1 unit. Since there exists a horizontal line intersecting the graph more than once,
shifted left 1 unit. Since there exists a horizontal line intersecting the graph more than once, 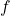 is not one-to-one.
is not one-to-one.

- On the interval
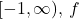 is one-to-one.
is one-to-one.

The domain and range of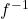 are given by the range and domain of
are given by the range and domain of 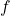 , respectively. Therefore, the domain of
, respectively. Therefore, the domain of 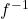 is
is 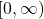 and the range of
and the range of 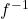 is
is 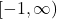 . To find a formula for
. To find a formula for 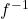 , solve the equation
, solve the equation 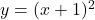 for
for 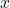 . If
. If 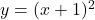 , then
, then 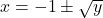 . Since we are restricting the domain to the interval where
. Since we are restricting the domain to the interval where  , we need
, we need 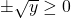 . Therefore,
. Therefore, 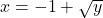 . Interchanging
. Interchanging  and
and 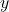 , we write
, we write 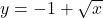 and conclude that
and conclude that 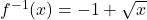 .
.
Consider ![]() restricted to the domain
restricted to the domain ![]() . Verify that
. Verify that ![]() is one-to-one on this domain. Determine the domain and range of the inverse of
is one-to-one on this domain. Determine the domain and range of the inverse of ![]() and find a formula for
and find a formula for ![]() .
.
Hint
The domain and range of ![]() is given by the range and domain of
is given by the range and domain of ![]() , respectively. To find
, respectively. To find ![]() , solve
, solve ![]() for
for ![]() .
.
Solution
The domain of ![]() is
is ![]() . The range of
. The range of ![]() is
is ![]() . The inverse function is given by the formula
. The inverse function is given by the formula ![]() .
.
Inverse Trigonometric Functions
The six basic trigonometric functions are periodic, and therefore they are not one-to-one. However, if we restrict the domain of a trigonometric function to an interval where it is one-to-one, we can define its inverse. Consider the sine function ( (Figure) ). The sine function is one-to-one on an infinite number of intervals, but the standard convention is to restrict the domain to the interval ![]() . By doing so, we define the inverse sine function on the domain
. By doing so, we define the inverse sine function on the domain ![]() such that for any
such that for any ![]() in the interval
in the interval ![]() , the inverse sine function tells us which angle
, the inverse sine function tells us which angle ![]() in the interval
in the interval ![]() satisfies
satisfies ![]() . Similarly, we can restrict the domains of the other trigonometric functions to define i nverse trigonometric functions , which are functions that tell us which angle in a certain interval has a specified trigonometric value.
. Similarly, we can restrict the domains of the other trigonometric functions to define i nverse trigonometric functions , which are functions that tell us which angle in a certain interval has a specified trigonometric value.
Definition
The inverse sine function, denoted ![]() or arcsin, and the inverse cosine function, denoted
or arcsin, and the inverse cosine function, denoted ![]() or arccos, are defined on the domain
or arccos, are defined on the domain ![]() as follows:
as follows:
The inverse tangent function, denoted ![]() or arctan, and inverse cotangent function, denoted
or arctan, and inverse cotangent function, denoted ![]() or arccot, are defined on the domain
or arccot, are defined on the domain ![]() as follows:
as follows:
The inverse cosecant function, denoted ![]() or arccsc, and inverse secant function, denoted
or arccsc, and inverse secant function, denoted ![]() or arcsec, are defined on the domain
or arcsec, are defined on the domain ![]() as follows:
as follows:
To graph the inverse trigonometric functions, we use the graphs of the trigonometric functions restricted to the domains defined earlier and reflect the graphs about the line ![]() ( (Figure) ).
( (Figure) ).

Go to the following site for more comparisons of functions and their inverses.
When evaluating an inverse trigonometric function, the output is an angle. For example, to evaluate ![]() , we need to find an angle
, we need to find an angle ![]() such that
such that ![]() . Clearly, many angles have this property. However, given the definition of
. Clearly, many angles have this property. However, given the definition of ![]() , we need the angle
, we need the angle ![]() that not only solves this equation, but also lies in the interval
that not only solves this equation, but also lies in the interval ![]() . We conclude that
. We conclude that ![]() .
.
We now consider a composition of a trigonometric function and its inverse. For example, consider the two expressions ![]() and
and ![]() . For the first one, we simplify as follows:
. For the first one, we simplify as follows:
For the second one, we have
The inverse function is supposed to “undo” the original function, so why isn’t ![]() ? Recalling our definition of inverse functions, a function
? Recalling our definition of inverse functions, a function ![]() and its inverse
and its inverse ![]() satisfy the conditions
satisfy the conditions ![]() for all
for all ![]() in the domain of
in the domain of ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() , so what happened here? The issue is that the inverse sine function,
, so what happened here? The issue is that the inverse sine function, ![]() , is the inverse of the restricted sine function defined on the domain
, is the inverse of the restricted sine function defined on the domain ![]() . Therefore, for
. Therefore, for ![]() in the interval
in the interval ![]() , it is true that
, it is true that ![]() . However, for values of
. However, for values of ![]() outside this interval, the equation does not hold, even though
outside this interval, the equation does not hold, even though ![]() is defined for all real numbers
is defined for all real numbers ![]() .
.
What about ![]() ? Does that have a similar issue? The answer is no . Since the domain of
? Does that have a similar issue? The answer is no . Since the domain of ![]() is the interval
is the interval ![]() , we conclude that
, we conclude that ![]() if
if ![]() and the expression is not defined for other values of
and the expression is not defined for other values of ![]() . To summarize,
. To summarize,
and
Similarly, for the cosine function,
and
Similar properties hold for the other trigonometric functions and their inverses.
Evaluating Expressions Involving Inverse Trigonometric Functions
Evaluate each of the following expressions.
Solution
- Evaluating
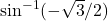 is equivalent to finding the angle
is equivalent to finding the angle 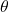 such that
such that 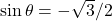 and
and 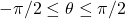 . The angle
. The angle 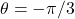 satisfies these two conditions. Therefore,
satisfies these two conditions. Therefore, 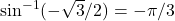 .
. - First we use the fact that
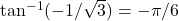 . Then
. Then 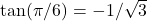 . Therefore,
. Therefore, 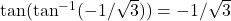 .
. - To evaluate
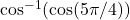 , first use the fact that
, first use the fact that 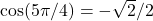 . Then we need to find the angle
. Then we need to find the angle 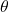 such that
such that 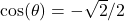 and
and 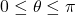 . Since
. Since 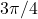 satisfies both these conditions, we have
satisfies both these conditions, we have 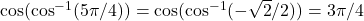 .
. - Since
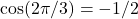 , we need to evaluate
, we need to evaluate 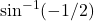 . That is, we need to find the angle
. That is, we need to find the angle 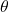 such that
such that 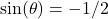 and
and 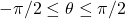 . Since
. Since 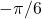 satisfies both these conditions, we can conclude that
satisfies both these conditions, we can conclude that 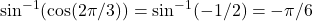 .
.
The Maximum Value of a Function
In many areas of science, engineering, and mathematics, it is useful to know the maximum value a function can obtain, even if we don’t know its exact value at a given instant. For instance, if we have a function describing the strength of a roof beam, we would want to know the maximum weight the beam can support without breaking. If we have a function that describes the speed of a train, we would want to know its maximum speed before it jumps off the rails. Safe design often depends on knowing maximum values.
This project describes a simple example of a function with a maximum value that depends on two equation coefficients. We will see that maximum values can depend on several factors other than the independent variable ![]() .
.
- Consider the graph in (Figure) of the function
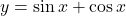 . Describe its overall shape. Is it periodic? How do you know?
. Describe its overall shape. Is it periodic? How do you know?

Using a graphing calculator or other graphing device, estimate the
 – and
– and 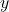 -values of the maximum point for the graph (the first such point where
-values of the maximum point for the graph (the first such point where 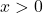 ). It may be helpful to express the
). It may be helpful to express the 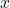 -value as a multiple of
-value as a multiple of 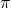 .
. - Now consider other graphs of the form
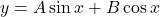 for various values of
for various values of 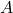 and
and 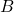 . Sketch the graph when
. Sketch the graph when 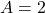 and
and 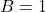 , and find the
, and find the 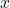 – and
– and 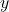 -values for the maximum point. (Remember to express the
-values for the maximum point. (Remember to express the 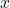 -value as a multiple of
-value as a multiple of 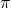 , if possible.) Has it moved?
, if possible.) Has it moved? - Repeat for
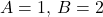 . Is there any relationship to what you found in part (2)?
. Is there any relationship to what you found in part (2)? - Complete the following table, adding a few choices of your own for
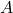 and
and 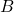 :
:
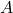
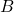
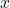
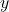
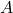
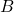
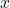
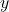
0 1 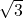
1 1 0 1 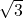
1 1 12 5 1 2 5 12 2 1 2 2 3 4 4 3 - Try to figure out the formula for the
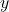 -values.
-values. - The formula for the
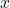 -values is a little harder. The most helpful points from the table are
-values is a little harder. The most helpful points from the table are 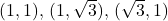 . ( Hint : Consider inverse trigonometric functions.)
. ( Hint : Consider inverse trigonometric functions.) - If you found formulas for parts (5) and (6), show that they work together. That is, substitute the
 -value formula you found into
-value formula you found into  and simplify it to arrive at the
and simplify it to arrive at the 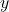 -value formula you found.
-value formula you found.
Key Concepts
- For a function to have an inverse, the function must be one-to-one. Given the graph of a function, we can determine whether the function is one-to-one by using the horizontal line test.
- If a function is not one-to-one, we can restrict the domain to a smaller domain where the function is one-to-one and then define the inverse of the function on the smaller domain.
- For a function
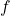 and its inverse
and its inverse 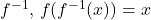 for all
for all 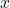 in the domain of
in the domain of 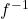 and
and 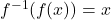 for all
for all 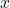 in the domain of
in the domain of 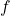 .
. - Since the trigonometric functions are periodic, we need to restrict their domains to define the inverse trigonometric functions.
- The graph of a function
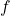 and its inverse
and its inverse 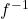 are symmetric about the line
are symmetric about the line 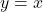 .
.
Key Equations
- Inverse functions
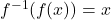 for all
for all 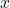 in
in 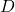 , and
, and 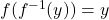 for all
for all 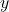 in
in 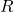 .[/latex]
.[/latex]
For the following exercises, use the horizontal line test to determine whether each of the given graphs is one-to-one.
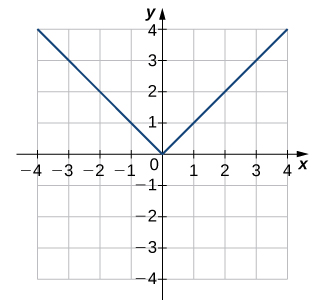
Solution
Not one-to-one
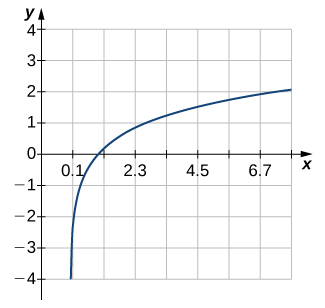
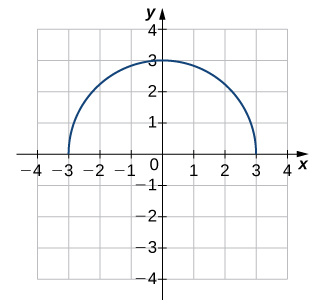
Solution
Not one-to-one
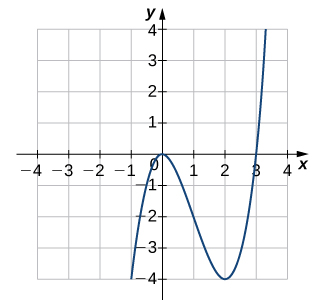
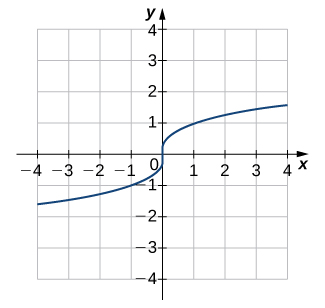
Solution
One-to-one
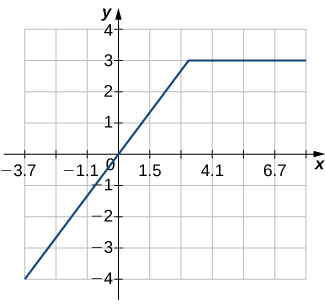
For the following exercises, a. find the inverse function, and b. find the domain and range of the inverse function.
7. ![]()
Solution
a. ![]() b. Domain:
b. Domain: ![]() , Range:
, Range: ![]()
8. ![]()
9. ![]()
Solution
a. ![]() b. Domain: all real numbers, Range: all real numbers
b. Domain: all real numbers, Range: all real numbers
10. ![]()
11. ![]()
Solution
a. ![]() , b. Domain:
, b. Domain: ![]() , Range:
, Range: ![]()
12. ![]()
13. ![]()
Solution
a. ![]() , b. Domain:
, b. Domain: ![]() , Range:
, Range: ![]()
14. ![]()
For the following exercises, use the graph of ![]() to sketch the graph of its inverse function.
to sketch the graph of its inverse function.
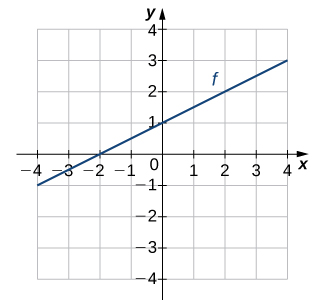
Solution

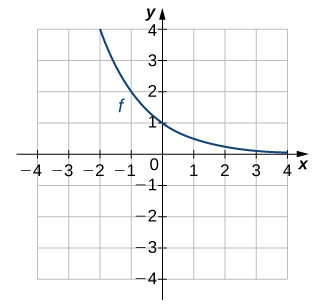
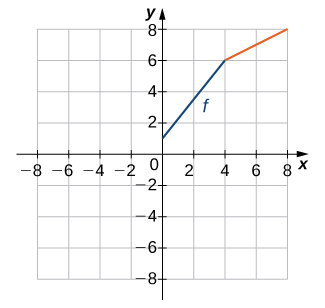
Solution

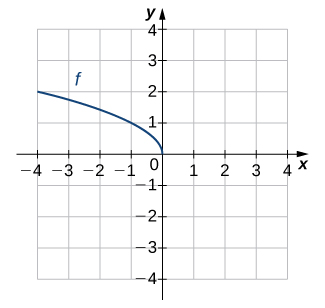
For the following exercises, use composition to determine which pairs of functions are inverses.
19. ![]()
Solution
These are inverses.
20. ![]()
21. ![]()
Solution
These are not inverses.
22. ![]()
23. ![]()
Solution
These are inverses.
24. ![]()
25. ![]()
Solution
These are inverses.
26. ![]()
For the following exercises, evaluate the functions. Give the exact value.
27. ![]()
Solution
![]()
28. ![]()
29. ![]()
Solution
![]()
30. ![]()
31. ![]()
Solution
![]()
32. ![]()
33. ![]()
34. ![]()
35. ![]()
Solution
![]()
36. The function ![]() converts degrees Fahrenheit to degrees Celsius.
converts degrees Fahrenheit to degrees Celsius.
- Find the inverse function
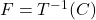
- What is the inverse function used for?
37. [T] The velocity ![]() (in centimeters per second) of blood in an artery at a distance
(in centimeters per second) of blood in an artery at a distance ![]() cm from the center of the artery can be modeled by the function
cm from the center of the artery can be modeled by the function ![]() for
for ![]() .
.
- Find
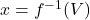 .
. - Interpret what the inverse function is used for.
- Find the distance from the center of an artery with a velocity of 15 cm/sec, 10 cm/sec, and 5 cm/sec.
Solution
a. ![]() b. The inverse function determines the distance from the center of the artery at which blood is flowing with velocity
b. The inverse function determines the distance from the center of the artery at which blood is flowing with velocity ![]() . c. 0.1 cm; 0.14 cm; 0.17 cm
. c. 0.1 cm; 0.14 cm; 0.17 cm
38. A function that converts dress sizes in the United States to those in Europe is given by ![]() .
.
- Find the European dress sizes that correspond to sizes 6, 8, 10, and 12 in the United States.
- Find the function that converts European dress sizes to U.S. dress sizes.
- Use part b. to find the dress sizes in the United States that correspond to 46, 52, 62, and 70.
39. [T] The cost to remove a toxin from a lake is modeled by the function
![]() , where
, where ![]() is the cost (in thousands of dollars) and
is the cost (in thousands of dollars) and ![]() is the amount of toxin in a small lake (measured in parts per billion [ppb]). This model is valid only when the amount of toxin is less than 85 ppb.
is the amount of toxin in a small lake (measured in parts per billion [ppb]). This model is valid only when the amount of toxin is less than 85 ppb.
- Find the cost to remove 25 ppb, 40 ppb, and 50 ppb of the toxin from the lake.
- Find the inverse function. c. Use part b. to determine how much of the toxin is removed for $50,000.
Solution
a. $31,250, $66,667, $107,143 b. ![]() c. 34 ppb
c. 34 ppb
40. [T] A race car is accelerating at a velocity given by
![]() ,
,
where ![]() is the velocity (in feet per second) at time
is the velocity (in feet per second) at time ![]() .
.
- Find the velocity of the car at 10 sec.
- Find the inverse function.
- Use part b. to determine how long it takes for the car to reach a speed of 150 ft/sec.
41. [T] An airplane’s Mach number ![]() is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by
is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by ![]() .
.
Find the Mach angle (to the nearest degree) for the following Mach numbers.
 1.0”.
1.0”.
Solution
a. ![]() b.
b. ![]() c.
c. ![]()
42. [T] Using ![]() , find the Mach number
, find the Mach number ![]() for the following angles.
for the following angles.
43. [T] The temperature (in degrees Celsius) of a city in the northern United States can be modeled by the function
![]() ,
,
where ![]() is time in months and
is time in months and ![]() corresponds to January 1. Determine the month and day when the temperature is
corresponds to January 1. Determine the month and day when the temperature is ![]() C.
C.
Solution
![]() ; so, the temperature occurs on June 21 and August 15
; so, the temperature occurs on June 21 and August 15
44. [T] The depth (in feet) of water at a dock changes with the rise and fall of tides. It is modeled by the function
![]() ,
,
where ![]() is the number of hours after midnight. Determine the first time after midnight when the depth is 11.75 ft.
is the number of hours after midnight. Determine the first time after midnight when the depth is 11.75 ft.
45. [T] An object moving in simple harmonic motion is modeled by the function
![]() ,
,
where ![]() is measured in inches and
is measured in inches and ![]() is measured in seconds. Determine the first time when the distance moved is 4.5 in.
is measured in seconds. Determine the first time when the distance moved is 4.5 in.
Solution
![]()
46. [T] A local art gallery has a portrait 3 ft in height that is hung 2.5 ft above the eye level of an average person. The viewing angle ![]() can be modeled by the function
can be modeled by the function
![]() ,
,
where ![]() is the distance (in feet) from the portrait. Find the viewing angle when a person is 4 ft from the portrait.
is the distance (in feet) from the portrait. Find the viewing angle when a person is 4 ft from the portrait.
47. [T] Use a calculator to evaluate ![]() and
and ![]() . Explain the results of each.
. Explain the results of each.
Solution
![]() ; the expression does not equal 2.1 since
; the expression does not equal 2.1 since ![]() —in other words, it is not in the restricted domain of
—in other words, it is not in the restricted domain of ![]() .
. ![]() , since 2.1 is in the restricted domain of
, since 2.1 is in the restricted domain of ![]() .
.
48. [T] Use a calculator to evaluate ![]() and
and ![]() . Explain the results of each.
. Explain the results of each.
Glossary
- horizontal line test
- a function
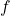 is one-to-one if and only if every horizontal line intersects the graph of
is one-to-one if and only if every horizontal line intersects the graph of 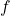 , at most, once
, at most, once
- inverse function
- for a function
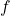 , the inverse function
, the inverse function 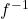 satisfies
satisfies 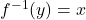 if
if 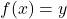
- inverse trigonometric functions
- the inverses of the trigonometric functions are defined on restricted domains where they are one-to-one functions
- one-to-one function
- a function
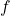 is one-to-one if
is one-to-one if 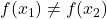 if
if 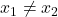
- restricted domain
- a subset of the domain of a function