8
Learning Objectives
- Calculate the limit of a function as
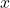 increases or decreases without bound.
increases or decreases without bound. - Recognize a horizontal asymptote on the graph of a function.
- Estimate the end behavior of a function as
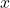 increases or decreases without bound.
increases or decreases without bound. - Recognize an oblique asymptote on the graph of a function.
To graph a function ![]() defined on an unbounded domain, we also need to know the behavior of
defined on an unbounded domain, we also need to know the behavior of ![]() as
as ![]() In this section, we define limits at infinity and show how these limits affect the graph of a function.
In this section, we define limits at infinity and show how these limits affect the graph of a function.
Limits at Infinity
We begin by examining what it means for a function to have a finite limit at infinity. Then we study the idea of a function with an infinite limit at infinity. Back in Introduction to Functions and Graphs, we looked at vertical asymptotes; in this section we deal with horizontal and oblique asymptotes.
Limits at Infinity and Horizontal Asymptotes
Recall that ![]() means
means ![]() becomes arbitrarily close to
becomes arbitrarily close to ![]() as long as
as long as ![]() is sufficiently close to
is sufficiently close to ![]() We can extend this idea to limits at infinity. For example, consider the function
We can extend this idea to limits at infinity. For example, consider the function ![]() As can be seen graphically in (Figure) and numerically in (Figure), as the values of
As can be seen graphically in (Figure) and numerically in (Figure), as the values of ![]() get larger, the values of
get larger, the values of ![]() approach 2. We say the limit as
approach 2. We say the limit as ![]() approaches
approaches ![]() of
of ![]() is 2 and write
is 2 and write ![]() Similarly, for
Similarly, for ![]() as the values
as the values ![]() get larger, the values of
get larger, the values of ![]() approaches 2. We say the limit as
approaches 2. We say the limit as ![]() approaches
approaches ![]() of
of ![]() is 2 and write
is 2 and write ![]()
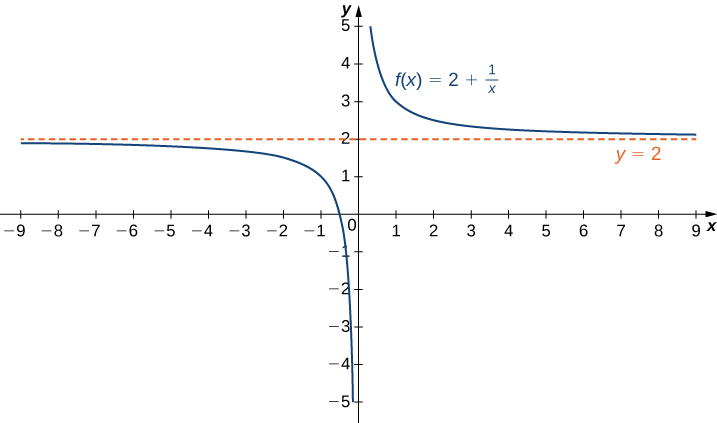
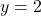 as
as 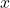 approaches
approaches 
| 10 | 100 | 1,000 | 10,000 | |
| 2.1 | 2.01 | 2.001 | 2.0001 | |
| -10 | -100 | -1000 | -10,000 | |
| 1.9 | 1.99 | 1.999 | 1.9999 |
More generally, for any function ![]() we say the limit as
we say the limit as ![]() of
of ![]() is
is ![]() if
if ![]() becomes arbitrarily close to
becomes arbitrarily close to ![]() as long as
as long as ![]() is sufficiently large. In that case, we write
is sufficiently large. In that case, we write ![]() Similarly, we say the limit as
Similarly, we say the limit as ![]() of
of ![]() is
is ![]() if
if ![]() becomes arbitrarily close to
becomes arbitrarily close to ![]() as long as
as long as ![]() and
and ![]() is sufficiently large. In that case, we write
is sufficiently large. In that case, we write ![]() We now look at the definition of a function having a limit at infinity.
We now look at the definition of a function having a limit at infinity.
Definition
(Informal) If the values of ![]() become arbitrarily close to
become arbitrarily close to ![]() as
as ![]() becomes sufficiently large, we say the function
becomes sufficiently large, we say the function ![]() has a limit at infinity and write
has a limit at infinity and write
If the values of ![]() becomes arbitrarily close to
becomes arbitrarily close to ![]() for
for ![]() as
as ![]() becomes sufficiently large, we say that the function
becomes sufficiently large, we say that the function ![]() has a limit at negative infinity and write
has a limit at negative infinity and write
If the values ![]() are getting arbitrarily close to some finite value
are getting arbitrarily close to some finite value ![]() as
as ![]() or
or ![]() the graph of
the graph of ![]() approaches the line
approaches the line ![]() In that case, the line
In that case, the line ![]() is a horizontal asymptote of
is a horizontal asymptote of ![]() ((Figure)). For example, for the function
((Figure)). For example, for the function ![]() since
since ![]() the line
the line ![]() is a horizontal asymptote of
is a horizontal asymptote of ![]()
Definition
If ![]() or
or ![]() we say the line
we say the line ![]() is a horizontal asymptote of
is a horizontal asymptote of ![]()
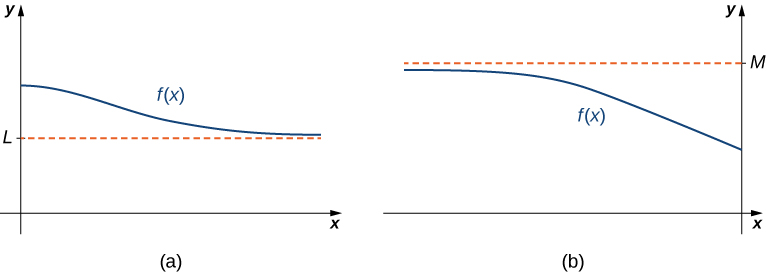
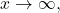 the values of
the values of 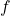 are getting arbitrarily close to
are getting arbitrarily close to 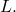 The line
The line 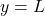 is a horizontal asymptote of
is a horizontal asymptote of 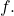 (b) As
(b) As 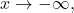 the values of
the values of 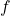 are getting arbitrarily close to
are getting arbitrarily close to 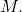 The line
The line 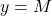 is a horizontal asymptote of
is a horizontal asymptote of 
A function cannot cross a vertical asymptote because the graph must approach infinity (or ![]() from at least one direction as
from at least one direction as ![]() approaches the vertical asymptote. However, a function may cross a horizontal asymptote. In fact, a function may cross a horizontal asymptote an unlimited number of times. For example, the function
approaches the vertical asymptote. However, a function may cross a horizontal asymptote. In fact, a function may cross a horizontal asymptote an unlimited number of times. For example, the function ![]() shown in (Figure) intersects the horizontal asymptote
shown in (Figure) intersects the horizontal asymptote ![]() an infinite number of times as it oscillates around the asymptote with ever-decreasing amplitude.
an infinite number of times as it oscillates around the asymptote with ever-decreasing amplitude.
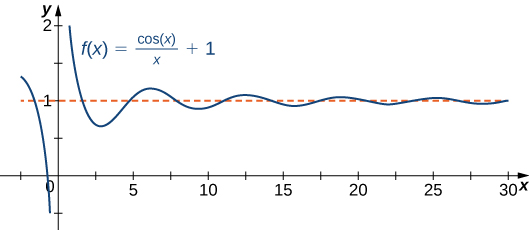
 crosses its horizontal asymptote
crosses its horizontal asymptote  an infinite number of times.
an infinite number of times.The algebraic limit laws and squeeze theorem we introduced in Introduction to Limits also apply to limits at infinity. We illustrate how to use these laws to compute several limits at infinity.
Computing Limits at Infinity
For each of the following functions ![]() evaluate
evaluate ![]() and
and ![]() Determine the horizontal asymptote(s) for
Determine the horizontal asymptote(s) for ![]()
Solution
- Using the algebraic limit laws, we have
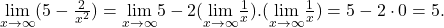 Similarly,
Similarly, 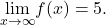 Therefore,
Therefore, 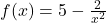 has a horizontal asymptote of
has a horizontal asymptote of 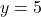 and
and 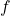 approaches this horizontal asymptote as
approaches this horizontal asymptote as 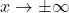 as shown in the following graph.
as shown in the following graph.
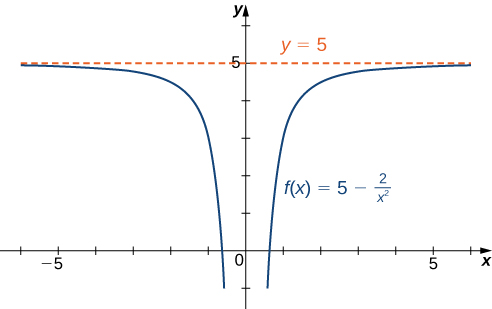
Figure 4. This function approaches a horizontal asymptote as 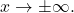
- Since
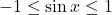 for all
for all  we have
we have
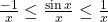
for all
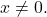 Also, since
Also, since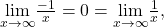
we can apply the squeeze theorem to conclude that
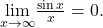
Similarly,
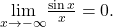
Thus,
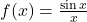 has a horizontal asymptote of
has a horizontal asymptote of 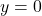 and
and 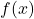 approaches this horizontal asymptote as
approaches this horizontal asymptote as 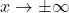 as shown in the following graph.
as shown in the following graph.
Figure 5. This function crosses its horizontal asymptote multiple times. - To evaluate
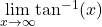 and
and 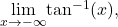 we first consider the graph of
we first consider the graph of 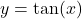 over the interval
over the interval 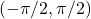 as shown in the following graph.
as shown in the following graph.
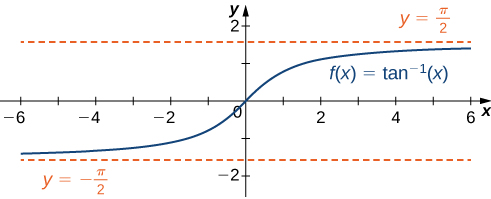
 The graph of
The graph of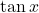 has vertical asymptotes at
has vertical asymptotes at 
Since
it follows that
Similarly, since
it follows that
As a result, ![]() and
and ![]() are horizontal asymptotes of
are horizontal asymptotes of ![]() as shown in the following graph.
as shown in the following graph.
Evaluate ![]() and
and ![]() Determine the horizontal asymptotes of
Determine the horizontal asymptotes of ![]() if any.
if any.
Hint
![]()
Solution
Both limits are 3. The line ![]() is a horizontal asymptote.
is a horizontal asymptote.
Infinite Limits at Infinity
Sometimes the values of a function ![]() become arbitrarily large as
become arbitrarily large as ![]() (or as
(or as ![]() In this case, we write
In this case, we write ![]() (or
(or ![]() On the other hand, if the values of
On the other hand, if the values of ![]() are negative but become arbitrarily large in magnitude as
are negative but become arbitrarily large in magnitude as ![]() (or as
(or as ![]() we write
we write ![]() (or
(or ![]()
For example, consider the function ![]() As seen in (Figure) and (Figure), as
As seen in (Figure) and (Figure), as ![]() the values
the values ![]() become arbitrarily large. Therefore,
become arbitrarily large. Therefore, ![]() On the other hand, as
On the other hand, as ![]() the values of
the values of ![]() are negative but become arbitrarily large in magnitude. Consequently,
are negative but become arbitrarily large in magnitude. Consequently, ![]()
| 10 | 20 | 50 | 100 | 1000 | |
| 1000 | 8000 | 125,000 | 1,000,000 | 1,000,000,000 | |
| -10 | -20 | -50 | -100 | -1000 | |
| -1000 | -8000 | -125,000 | -1,000,000 | -1,000,000,000 |
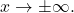
Definition
(Informal) We say a function ![]() has an infinite limit at infinity and write
has an infinite limit at infinity and write
if ![]() becomes arbitrarily large for
becomes arbitrarily large for ![]() sufficiently large. We say a function has a negative infinite limit at infinity and write
sufficiently large. We say a function has a negative infinite limit at infinity and write
if ![]() and
and ![]() becomes arbitrarily large for
becomes arbitrarily large for ![]() sufficiently large. Similarly, we can define infinite limits as
sufficiently large. Similarly, we can define infinite limits as ![]()
Formal Definitions
Earlier, we used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally. Although these terms provide accurate descriptions of limits at infinity, they are not precise mathematically. Here are more formal definitions of limits at infinity. We then look at how to use these definitions to prove results involving limits at infinity.
Definition
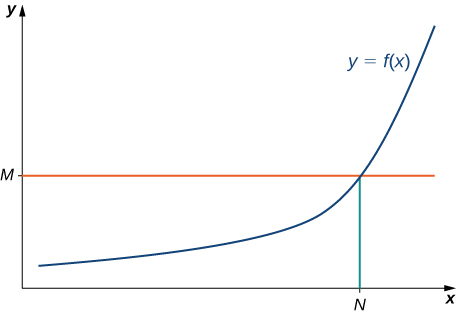
(Formal) We say a function ![]() has a limit at infinity, if there exists a real number
has a limit at infinity, if there exists a real number ![]() such that for all
such that for all ![]() there exists
there exists ![]() such that
such that
for all ![]() In that case, we write
In that case, we write
(see (Figure)).
We say a function ![]() has a limit at negative infinity if there exists a real number
has a limit at negative infinity if there exists a real number ![]() such that for all
such that for all ![]() there exists
there exists ![]() such that
such that
for all ![]() In that case, we write
In that case, we write
Earlier in this section, we used graphical evidence in (Figure) and numerical evidence in (Figure) to conclude that ![]() Here we use the formal definition of limit at infinity to prove this result rigorously.
Here we use the formal definition of limit at infinity to prove this result rigorously.
A Finite Limit at Infinity Example
Use the formal definition of limit at infinity to prove that ![]()
Solution
Let ![]() Let
Let ![]() Therefore, for all
Therefore, for all ![]() we have
we have
Use the formal definition of limit at infinity to prove that ![]()
Hint
Let ![]()
Solution
Let ![]() Let
Let ![]() Therefore, for all
Therefore, for all ![]() we have
we have
![]()
Therefore, ![]()
We now turn our attention to a more precise definition for an infinite limit at infinity.
Definition
(Formal) We say a function ![]() has an infinite limit at infinity and write
has an infinite limit at infinity and write
if for all ![]() there exists an
there exists an ![]() such that
such that
for all ![]() (see (Figure)).
(see (Figure)).
We say a function has a negative infinite limit at infinity and write
if for all ![]() there exists an
there exists an ![]() such that
such that
for all ![]()
Similarly we can define limits as ![]()
Earlier, we used graphical evidence ((Figure)) and numerical evidence ((Figure)) to conclude that ![]() Here we use the formal definition of infinite limit at infinity to prove that result.
Here we use the formal definition of infinite limit at infinity to prove that result.
An Infinite Limit at Infinity
Use the formal definition of infinite limit at infinity to prove that ![]()
Solution
Let ![]() Let
Let ![]() Then, for all
Then, for all ![]() we have
we have
Therefore, ![]()
Use the formal definition of infinite limit at infinity to prove that ![]()
Hint
Let ![]()
Solution
Let ![]() Let
Let ![]() Then, for all
Then, for all ![]() we have
we have
![]()
End Behavior
The behavior of a function as ![]() is called the function’s end behavior. At each of the function’s ends, the function could exhibit one of the following types of behavior:
is called the function’s end behavior. At each of the function’s ends, the function could exhibit one of the following types of behavior:
- The function
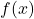 approaches a horizontal asymptote
approaches a horizontal asymptote 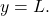
- The function
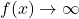 or
or 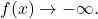
- The function does not approach a finite limit, nor does it approach
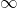 or
or  In this case, the function may have some oscillatory behavior.
In this case, the function may have some oscillatory behavior.
Let’s consider several classes of functions here and look at the different types of end behaviors for these functions.
End Behavior for Polynomial Functions
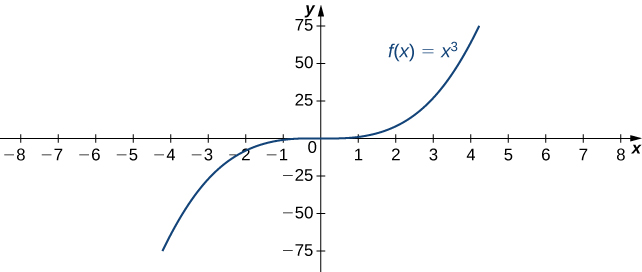
Consider the power function ![]() where
where ![]() is a positive integer. From (Figure) and (Figure), we see that
is a positive integer. From (Figure) and (Figure), we see that
and
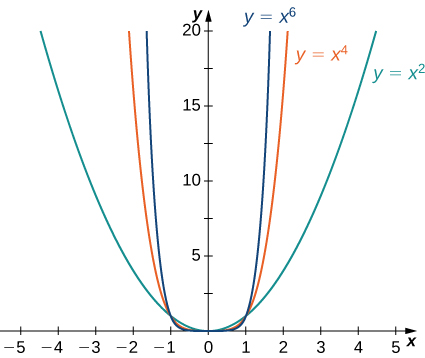
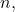
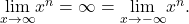
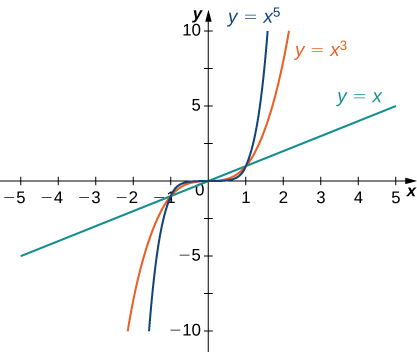
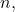
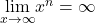 and
and 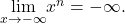
Using these facts, it is not difficult to evaluate ![]() and
and ![]() where
where ![]() is any constant and
is any constant and ![]() is a positive integer. If
is a positive integer. If ![]() the graph of
the graph of ![]() is a vertical stretch or compression of
is a vertical stretch or compression of ![]() and therefore
and therefore
If ![]() the graph of
the graph of ![]() is a vertical stretch or compression combined with a reflection about the
is a vertical stretch or compression combined with a reflection about the ![]() -axis, and therefore
-axis, and therefore
If ![]() in which case
in which case ![]()
Limits at Infinity for Power Functions
For each function ![]() evaluate
evaluate ![]() and
and ![]()
Solution
- Since the coefficient of
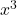 is -5, the graph of
is -5, the graph of 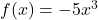 involves a vertical stretch and reflection of the graph of
involves a vertical stretch and reflection of the graph of 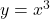 about the
about the 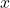 -axis. Therefore,
-axis. Therefore, 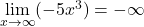 and
and 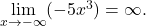
- Since the coefficient of
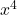 is 2, the graph of
is 2, the graph of 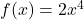 is a vertical stretch of the graph of
is a vertical stretch of the graph of 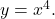 Therefore,
Therefore, 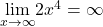 and
and 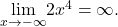
- This is an
 form so limit laws don’t help. However, by factoring we get
form so limit laws don’t help. However, by factoring we get
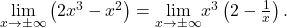 As
As 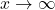 , the power
, the power 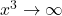 where the second factor gets close to
where the second factor gets close to 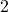 . Hence the limit is
. Hence the limit is 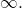 As
As 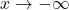 , the power
, the power 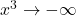 where the second factor gets close to
where the second factor gets close to 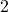 . Hence the limit is
. Hence the limit is 
Let ![]() Find
Find ![]()
Hint
The coefficient -3 is negative.
Solution
![]()
End Behavior for Algebraic Functions
The end behavior for rational functions and functions involving radicals is a little more complicated than for polynomials. To evaluate the limits at infinity for a rational function, we divide the numerator and denominator by the highest power of ![]() appearing in the denominator. This determines which term in the overall expression dominates the behavior of the function at large values of
appearing in the denominator. This determines which term in the overall expression dominates the behavior of the function at large values of ![]()
Determining End Behavior for Rational Functions
For each of the following functions, determine the limits as ![]() and
and ![]() Then, use this information to describe the end behavior of the function.
Then, use this information to describe the end behavior of the function.
Solution
- The highest power of
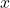 in the denominator is
in the denominator is 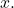 Therefore, dividing the numerator and denominator by
Therefore, dividing the numerator and denominator by 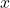 and applying the algebraic limit laws, we see that
and applying the algebraic limit laws, we see that
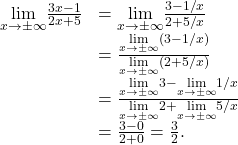
Since
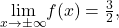 we know that
we know that  is a horizontal asymptote for this function as shown in the following graph.
is a horizontal asymptote for this function as shown in the following graph.
Figure 14. The graph of this rational function approaches a horizontal asymptote as 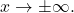
- Since the largest power of
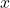 appearing in the denominator is
appearing in the denominator is 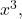 divide the numerator and denominator by
divide the numerator and denominator by 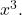 After doing so and applying algebraic limit laws, we obtain
After doing so and applying algebraic limit laws, we obtain
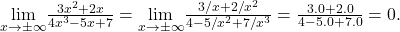
Therefore
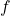 has a horizontal asymptote of
has a horizontal asymptote of 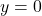 as shown in the following graph.
as shown in the following graph.
Figure 15. The graph of this rational function approaches the horizontal asymptote 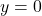 as
as 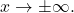
- Dividing the numerator and denominator by
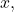 we have
we have
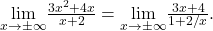
As
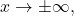 the denominator approaches 1. As
the denominator approaches 1. As 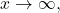 the numerator approaches
the numerator approaches 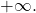 As
As 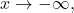 the numerator approaches
the numerator approaches  Therefore
Therefore 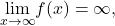 whereas
whereas 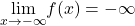 as shown in the following figure.
as shown in the following figure.
Figure 16. As 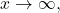 the values
the values 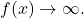 As
As 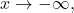 the values
the values 
Evaluate ![]() and use these limits to determine the end behavior of
and use these limits to determine the end behavior of ![]()
Hint
Divide the numerator and denominator by ![]()
Solution
![]()
Before proceeding, consider the graph of ![]() shown in (Figure). As
shown in (Figure). As ![]() and
and ![]() the graph of
the graph of ![]() appears almost linear. Although
appears almost linear. Although ![]() is certainly not a linear function, we now investigate why the graph of
is certainly not a linear function, we now investigate why the graph of ![]() seems to be approaching a linear function. First, using long division of polynomials, we can write
seems to be approaching a linear function. First, using long division of polynomials, we can write
Since ![]() as
as ![]() we conclude that
we conclude that
Therefore, the graph of ![]() approaches the line
approaches the line ![]() as
as ![]() This line is known as an oblique asymptote for
This line is known as an oblique asymptote for ![]() ((Figure)).
((Figure)).
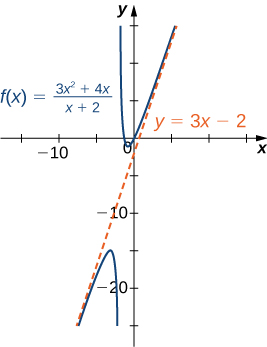
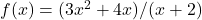 approaches the oblique asymptote
approaches the oblique asymptote 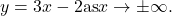
Now let’s consider the end behavior for functions involving a radical.
Determining End Behavior for a Function Involving a Radical
Find the limits as ![]() and
and ![]() for
for ![]() and describe the end behavior of
and describe the end behavior of ![]()
Solution
Let’s use the same strategy as we did for rational functions: divide the numerator and denominator by a power of ![]() To determine the appropriate power of
To determine the appropriate power of ![]() consider the expression
consider the expression ![]() in the denominator. Since
in the denominator. Since
for large values of ![]() in effect
in effect ![]() appears just to the first power in the denominator. Therefore, we divide the numerator and denominator by
appears just to the first power in the denominator. Therefore, we divide the numerator and denominator by ![]() Then, using the fact that
Then, using the fact that ![]() for
for ![]()
![]() for
for ![]() and
and ![]() for all
for all ![]() we calculate the limits as follows:
we calculate the limits as follows:
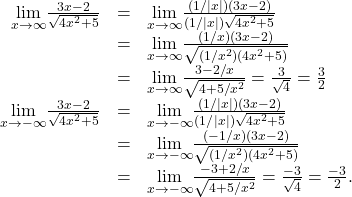
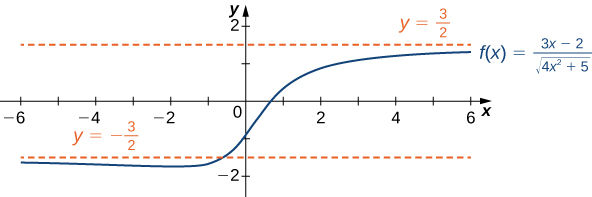
Therefore, ![]() approaches the horizontal asymptote
approaches the horizontal asymptote ![]() as
as ![]() and the horizontal asymptote
and the horizontal asymptote ![]() as
as ![]() as shown in the following graph.
as shown in the following graph.
Evaluate ![]()
Hint
Divide the numerator and denominator by ![]()
Solution
![]()
Determining End Behavior for Transcendental Functions
The six basic trigonometric functions are periodic and do not approach a finite limit as ![]() For example,
For example, ![]() oscillates between
oscillates between ![]() ((Figure)). The tangent function
((Figure)). The tangent function ![]() has an infinite number of vertical asymptotes as
has an infinite number of vertical asymptotes as ![]() therefore, it does not approach a finite limit nor does it approach
therefore, it does not approach a finite limit nor does it approach ![]() as
as ![]() as shown in (Figure).
as shown in (Figure).
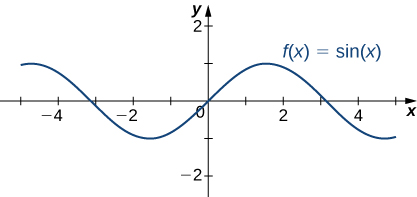
 oscillates between
oscillates between  as
as 
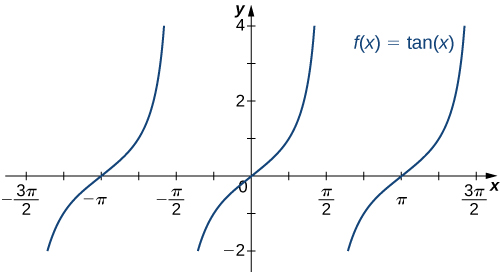
 does not approach a limit and does not approach
does not approach a limit and does not approach  as
as 
Recall that for any base ![]() the function
the function ![]() is an exponential function with domain
is an exponential function with domain ![]() and range
and range ![]() If
If ![]() is increasing over
is increasing over ![]() If
If ![]()
![]() is decreasing over
is decreasing over ![]() For the natural exponential function
For the natural exponential function ![]()
![]() Therefore,
Therefore, ![]() is increasing on
is increasing on ![]() and the range is
and the range is ![]() The exponential function
The exponential function ![]() approaches
approaches ![]() as
as ![]() and approaches 0 as
and approaches 0 as ![]() as shown in (Figure) and (Figure).
as shown in (Figure) and (Figure).
| -5 | -2 | 0 | 2 | 5 | |
| 0.00674 | 0.135 | 1 | 7.389 | 148.413 |
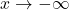 and approaches
and approaches  as
as 
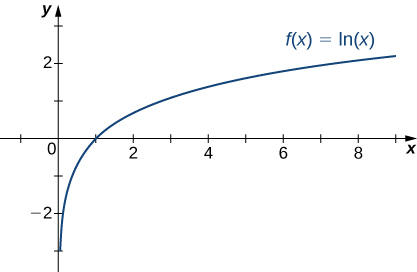
Recall that the natural logarithm function ![]() is the inverse of the natural exponential function
is the inverse of the natural exponential function ![]() Therefore, the domain of
Therefore, the domain of ![]() is
is ![]() and the range is
and the range is ![]() The graph of
The graph of ![]() is the reflection of the graph of
is the reflection of the graph of ![]() about the line
about the line ![]() Therefore,
Therefore, ![]() as
as ![]() and
and ![]() as
as ![]() as shown in (Figure) and (Figure).
as shown in (Figure) and (Figure).
| 0.01 | 0.1 | 1 | 10 | 100 | |
| -4.605 | -2.303 | 0 | 2.303 | 4.605 |
 as
as 
Determining End Behavior for a Transcendental Function
Find the limits as ![]() and
and ![]() for
for ![]() and describe the end behavior of
and describe the end behavior of ![]()
Solution
To find the limit as ![]() divide the numerator and denominator by
divide the numerator and denominator by ![]()
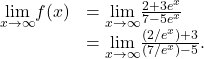
As shown in (Figure), ![]() as
as ![]() Therefore,
Therefore,
We conclude that ![]() and the graph of
and the graph of ![]() approaches the horizontal asymptote
approaches the horizontal asymptote ![]() as
as ![]() To find the limit as
To find the limit as ![]() use the fact that
use the fact that ![]() as
as ![]() to conclude that
to conclude that ![]() and therefore the graph of approaches the horizontal asymptote
and therefore the graph of approaches the horizontal asymptote ![]() as
as ![]()
Find the limits as ![]() and
and ![]() for
for ![]()
Hint
![]() and
and ![]()
Solution
![]() ,
, ![]()
Key Concepts
- The limit of
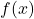 is
is 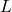 as
as 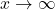 (or as
(or as 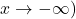 if the values
if the values 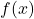 become arbitrarily close to
become arbitrarily close to 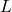 as
as 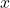 becomes sufficiently large.
becomes sufficiently large. - The limit of
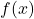 is
is 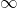 as
as 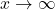 if
if 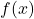 becomes arbitrarily large as
becomes arbitrarily large as 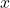 becomes sufficiently large. The limit of
becomes sufficiently large. The limit of 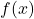 is
is  as
as 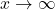 if
if 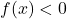 and
and 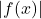 becomes arbitrarily large as
becomes arbitrarily large as 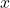 becomes sufficiently large. We can define the limit of
becomes sufficiently large. We can define the limit of 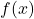 as
as 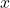 approaches
approaches  similarly.
similarly.
For the following exercises, examine the graphs. Identify where the vertical asymptotes are located.
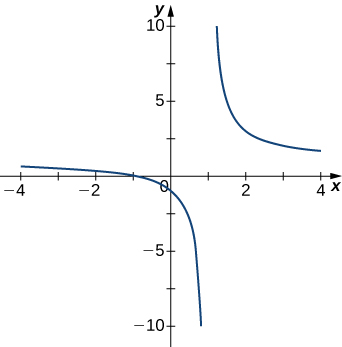
Solution
![]()
Solution
![]()
Solution
![]()
For the following functions ![]() determine whether there is an asymptote at
determine whether there is an asymptote at ![]() Justify your answer without graphing on a calculator.
Justify your answer without graphing on a calculator.
6. ![]()
7. ![]()
Solution
Yes, there is a vertical asymptote
8. ![]()
9. ![]()
Solution
Yes, there is vertical asymptote
10. ![]()
For the following exercises, evaluate the limit.
11. ![]()
Solution
0
12. ![]()
13. ![]()
Solution
![]()
14. ![]()
15. ![]()
Solution
![]()
16. ![]()
17. ![]()
Solution
-2
18. ![]()
19. ![]()
Solution
-4
20. ![]()
21. ![]()
Solution
![]()
22. ![]()
23. ![]()
Solution
![]()
24. ![]()
For the following exercises, find the horizontal and vertical asymptotes.
25. ![]()
Solution
Horizontal: none, vertical: ![]()
26. ![]()
27. ![]()
Solution
Horizontal: none, vertical: ![]()
28. ![]()
29. ![]()
Solution
Horizontal: none, vertical: none
30. ![]()
31. ![]()
Solution
Horizontal: ![]() vertical:
vertical: ![]()
32. ![]()
33. ![]()
Solution
Horizontal: ![]() vertical:
vertical: ![]() and
and ![]()
34. ![]()
35. ![]()
Solution
Horizontal: ![]() vertical:
vertical: ![]()
36. ![]()
37. ![]()
Solution
Horizontal: none, vertical: none
38. ![]()
39. ![]()
Solution
Horizontal: ![]() , vertical:
, vertical: ![]()
40. ![]()
For the following exercises, construct a function ![]() that has the given asymptotes.
that has the given asymptotes.
41. ![]() and
and ![]()
Solution
Answers will vary, for example: ![]()
42. ![]() and
and ![]()
43. ![]() and
and ![]()
Solution
Answers will vary, for example: ![]()
44. ![]()
For the following exercises, graph the function on a graphing calculator on the window ![]() and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
45. [T]![]()
Solution
![]()
46. [T]![]()
47. [T]![]()
Solution
![]()
48. [T]![]()
49. [T]![]()
Solution
![]()
50. True or false: Every ratio of polynomials has vertical asymptotes.
Glossary
- end behavior
- the behavior of a function as
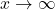 and
and 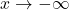
- horizontal asymptote
- if
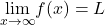 or
or 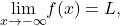 then
then 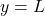 is a horizontal asymptote of
is a horizontal asymptote of 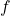
- infinite limit at infinity
- a function that becomes arbitrarily large as
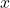 becomes large
becomes large
- limit at infinity
- the limiting value, if it exists, of a function as
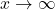 or
or 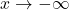
- oblique asymptote
- the line
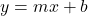 if
if 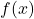 approaches it as
approaches it as 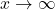 or
or